- Share
Where Would the Federal Funds Rate Be, If It Could Be Negative?
In the wake of Great Recession, the Federal Reserve engaged in conventional monetary policy actions by reducing the federal funds rate. But soon the rate hit zero, and could go no lower. In such environments, policymakers still think in terms of where the federal funds rate should be, were it possible to go negative. To project the “unconstrained path” of the funds rate—ignoring the zero lower bound—and to identify the key underlying shocks driving that path, we employ a statistical macroeconomic forecasting model. We find that the federal funds rate would have been extremely negative during 2009-2010.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
At the press conference following the April 2012 FOMC meeting, a reporter asked Chairman Bernanke where he thought the federal funds rate would be if it could go below zero. Bernanke replied that the answer would depend on the model used and the assumptions made. We attempt to address this question empirically by employing a particular statistical model.
As the U.S. economy showed signs of weakness in 2007, monetary policy actions reduced the federal funds rate by almost 100 basis points over the course of the year, from a high of 5.25 percent to 4.25 percent. These monetary policy actions, from most vantage points, appeared conventional and relatively comparable to the extent of the economic slowdown to that point.
In contrast, the financial crisis in the fall of 2008 coincided with the beginning of the sharpest and deepest contraction of the recession. In response, the Federal Reserve lowered the federal funds rate target to a range of 0 percent to 0.25 percent. The federal funds rate is a nominal interest rate and cannot go below zero, a constraint known as the zero lower bound (ZLB). Once the rate arrived at the bound, conventional monetary policy could do no more.
Yet the economy remained weak. Unemployment increased dramatically from 6.9 percent in 2008:Q4 (on a quarterly average basis) to a peak of 9.9 percent in 2009:Q4.
Similarly, real GDP contracted further in 2009. To address this weakness, the Federal Reserve turned to nonconventional policies, but researchers—and journalists—wonder what the path of the federal funds rate would have been under these circumstances, were it unconstrained by the ZLB. We use a model to project that path.
The type of model we employ is a statistical model of the U.S. economy that is estimated using quarterly macroeconomic and financial data from 1959 through 2008. It provides a statistical characterization of the way monetary policy typically responds to changes in the other variables in the model over this period. The model predicts that the unconstrained federal funds rate would have fallen far below the zero lower bound by as much as 5 to 6 percentage points
Conventional Monetary Policy Instrument
The Federal Reserve conducts conventional monetary policy by targeting the federal funds rate, the rate that banks charge each other for overnight loans of their reserves held with the Fed. The Federal Reserve can directly influence this rate because its transactions with private market banks affect the total supply of bank reserves. Banks are required to hold a minimum level of reserves against their deposits, and banks may borrow reserves to meet those requirements or to make additional loans to customers.
Monetary policy affects the real economy because the level of the federal funds rate sets the opportunity cost for additional funds for banks. The cost of these funds then influences the level of interest rates that banks charge customers for loans, as well as the level of other market interest rates. Higher interest rates (all other things the same) raise the cost of borrowing and tend to reduce loan and investment activity, whereas lower interest rates (all other things the same) reduce the cost of borrowing and tend to increase loan and investment activity.
Federal Reserve monetary policy aims to achieve its statutory goals of low inflation and maximum employment. This dual mandate has been often characterized as a balancing act—trying to achieve lower unemployment while maintaining low inflation. The frequent criticism of Fed policies reflects the difficulty of setting the “correct” federal funds rate to achieve these goals.
In past economic cycles, the level of the federal funds rate appears to have responded to movements in the rate of inflation as well as to movements in real output and unemployment. The popular Taylor rule characterizes monetary policy as responding to deviations from target inflation and deviations from potential output or the natural rate of unemployment. The monetary policy “reaction function” in the empirical model used in our analysis is more general, and characterizes monetary policy as responding to a larger set of variables. That said, the most important determinants of movements in the federal funds rate are real output and unemployment.1
The results and analysis that follow are dependent on the particular model that we use and the implied monetary policy rule embedded in it. That is, the same modeling techniques used on a different set of variables or over a different sample time period would likely generate results with greater or lesser magnitudes (and possibly different interpretations) of federal funds rate responses.
However, our statistical model of the economy is areasonable starting point for the analysis of this issue. This class of statistical models aims at characterizing the movements of the data series with minimal restrictions on the data interrelationships. As a result, the model used in our exercise can capture and illustrate various complex dynamic relationships among the variables of interest.
Forecasting Model
For the analysis, we employ a medium-scale version of a popular class of models used by macroeconomists for forecasting called Vector Autoregressive (VAR) models. VAR models consist of equations relating the current value of each variable to past values of all variables of the model including its own. These models capture historical statistical correlations between the variables of the model, and the model’s forecasts display the projection forward of these summarized correlations. The specific model that we use is the model described in Ken Beauchemin and Saeed Zaman’s paper, “A Medium Scale Forecasting Model for Monetary Policy.” It contains 17 variables (table 1), and to improve its forecast accuracy, it is estimated with prior restrictions imposed on the model’s parameters.2 These prior restrictions are known as Bayesian priors, and their use makes this model a BVAR.
Table 1. Model Variables
| Real gross domestic product |
| Real disposable income |
| Real consumption |
| Real private nonresidential investment: Equipment and software |
| PCE less food and energy: Chain price index |
| Personal consumption expenditures: Chain price index |
| PPI: Industrial commodities |
| Nonfarm business sector: Real output per hour of all persons |
| ECI: compensation: private industry workers |
| All employees: Total nonfarm |
| Unemployment rate |
| Federal funds rate |
| 10-year Treasury note yield at constant maturity |
| Moody’s seasoned Baa corporate bond yield |
| Stock price index: Standard & Poor’s 500 Composite |
| S&P: Composite 500, dividend yield |
| Nominal trade-weighted exchange value of U.S. vs. major currencies |
In this model, the monetary policy reaction function—the way monetary policy as measured by the federal funds rate responds to movements in other variables—is an implied one. That is, the reaction function is determined by the equation in the model that corresponds to the federal funds rate, which includes the lagged observations of all 17 variables in the BVAR.3 The BVAR reaction function contrasts with a Taylor rule in that the reaction function of monetary policy in the Taylor rule is explicitly characterized in terms of a small set of variables as noted above.
The Unconstrained Path of the Federal Funds Rate
We use this model to address the question of what the path of the federal funds rate might have been had the zero lower bound not been binding on policy. To do this, we estimate the model in a way that generates a “conditional” forecast of the federal funds rate in the wake of the Great Recession, representing the “unconstrained” path of the rate over this period.
Specifically, the exercise uses the model to compute a “forecast” for the federal funds rate path from the beginning of the recession to the second quarter of 2012. Unlike a standard, unconditional forecast, which would generate forecasts for future periods (starting in 2008:Q4) and subsequently employ forecast values for all variables for those periods as the forecast horizon extends out toward the end of the forecast sample, we plug in the actual values except for the federal funds rate. The mental experiment is the following: suppose we could know the values of all the other variables of our model in real time (no waiting for data gathering, reporting, and revising). Our model would tell us how the federal funds rate would typically respond to the evolving state of the economy—given the historical relationships as captured by our economic model.
First, we estimate the parameters for the 17 variables of the BVAR model using all the data from 1959:Q1 through 2008:Q3.4 Next, using the model with the estimated parameters, we forecast the federal funds rate for the next three years—14 quarters starting from 2008:Q4 to 2012:Q2.
Figure 1 shows the conditional forecast of the federal funds rate, with the mean forecast and the associated 70 and 90 percent probability bands. As the data following the financial crisis passes into the model, the forecast of the federal funds rate becomes negative immediately in 2009:Q1. It reaches its nadir of −5 percent in 2009:Q3. And by the end of 2012:Q2 it is −2 percent. Also included in the figure for reference purposes is the federal funds rate implied by a Taylor rule with core inflation and the unemployment gap.5 The trajectory of the fed funds rate implied by the Taylor rule is roughly similar to the model’s conditional forecast of the federal funds rate (it is within the 70 percent error bounds of the model).
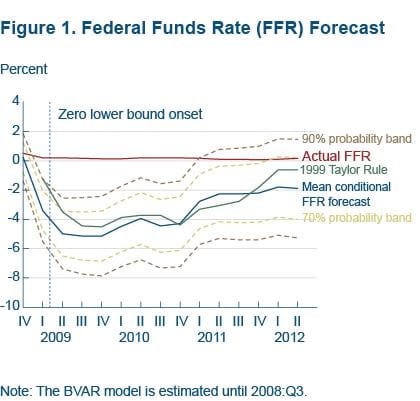
The model forecast of the funds rate turns negative in response to the severity of the economic contraction. The sharp movements in the other data series from 2008 onward called for substantial monetary accommodation. They implied a lowering of the federal funds rate by more than 500 basis points (from 0.25 percent in 2008:Q4 to −5 percent in 2009:Q3).
Underlying Sources of the Federal Funds Rate Path
The conditional forecast indicates how the model would have predicted the level of the funds rate in response to the actual observation of the other data series in the model. However, the forecast indicates the combined effect of the paths of these series on the funds rate forecast. We want to uncover the identity of the key variables that determined the outcome. To address this question, we estimate the model in a different way, one that generates an unconditional forecast.
The unconditional forecast as described above uses the actual values of data up to a given date—say 2008:Q3—to estimate the model and then generates forecasts of the future values of all the data series in the model. These forecasts are compared to actual values (not generated by the model), and the differences are analyzed to reveal the contribution of the different data series to the trajectory of the fed funds rate. (Recall that the conditional forecast employs actual values rather than forecasts for all variables except the federal funds rate.)
Economists refer to a “forecast error” as the difference between the actual data and the unconditional forecast. Forecast errors are typically correlated contemporaneously, meaning that forecast errors for real GDP and real consumption dated 2009:Q1 are (positively) correlated. Such an observation indicates how challenging it can be to identify whether a forecast error in real consumption arises from an inability to predict real consumption or an inability to predict real GDP or both. In order to get a sense of the underlying forces driving the federal funds rate forecast into negative territory, we decompose each variable’s forecast error into a function of all the uncorrelated “shocks” in the model.6
The forecast error of the federal funds rate is decomposed into the uncorrelated shocks of all 17 variables. This exercise, known as historical decomposition, involves forecasting the federal funds rate from 2008:Q4 through 2012:Q2 and computing the forecast errors. We can then distinguish the proportion of the forecast error that arises from each individual uncorrelated shock series.
Figure 2 plots the unconditional forecast of the federal funds rate using only data available through 2008:Q3; notice that this forecast falls slightly negative through most of 2009 and 2010 and reaches a trough of about −0.6 percent at 2010:Q1. The difference between the unconditional forecast and the actual federal funds rate is the forecast error measure described above.
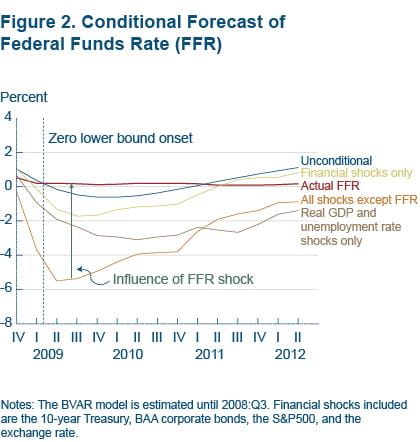
Using the actual data for all the other variables, we can decompose the source of the forecast errors for the fed funds rate. Specifically, we can isolate the contribution of the uncorrelated shocks associated with other variables (as well as for the federal funds rate) to the forecast error. We could plot 17 individual conditional forecast lines of the federal funds rate, each differing depending on which of the 17 shocks is added to the original unconditional funds rate forecast. But for the sake of brevity, we group the 17 shocks in three groups; one plot shows the conditional forecast of the federal funds rate due to financial shocks only (that is, the 10-year yield, the BAA yield, the SP500, the SP500 dividend yield, and the exchange rate); another shows the forecast with real GDP and the unemployment rate shocks only; and the last one shows the forecast of the federal funds rate due to all shocks except the fed funds rate shock. The orange line, therefore, introduces the additional knowledge of the shocks in all other variables in the model except for the orthogonal shock in the federal funds rate.
Roughly in line with the conditional forecast, historical decomposition suggests that as the financial crisis hit, the combined effect of the 16 shocks forces the federal funds rate significantly lower, to about −5.50 percent by 2009:Q2 (orange line). The magnitude and persistence of the combination of the 16 shocks force the fed funds rate significantly below zero throughout the sample period considered.
The arrow shows the direction of the fed funds rate shock. The zero lower bound constraint forces the shock associated with the federal funds rate to be positive and large. This outcome arises because the sum of influence of all the other shocks on the federal funds rate is negative and all the shocks (that is, the 17 including the federal funds rate) added to the unconditional funds rate forecast should sum to the red line representing the actual funds rate. Hence, the zero lower bound in this model imposes a severe restriction on the model outcome for the federal funds rate and implies what is effectively a monetary tightening.7
The relative contribution of the different data series to the federal funds rate forecast can be gauged by comparing the distance of each grouping’s conditional forecast to that of the forecast with all the shocks except the funds rate orange line). Real GDP and the unemployment rate contribute the most, and together they exert negative pressure on the funds rate forecast throughout the forecast period. From 2010:Q4 it is other variables, including the financial ones, that improve enough to pull the funds rate forecast above a plateau of around −4 percent. The financial variables contribute less than GDP and unemployment but still they account for a significant portion of the forecast path.
Unconventional Tools
Monetary policy makers have employed unconventional tools to mitigate the zero lower bound constraint. For example, some policies aim at lowering long-term interest rates through purchases of longer-term Treasury securities, agency debt, and mortgage-backed securities. The actions have been called large scale asset purchases, and the specific events have been referred to as quantitative easing, with acronyms QE1 and QE2. (A more recent policy with the same aim involves maturity exchanges—where the Fed sells short-term Treasury securities and buys long-term Treasury securities in the same dollar amount—and has been nicknamed Operation Twist.) Furthermore, communications strategies, such as providing forward guidance on the federal funds rate in regular FOMC statements and publishing interest rate forecasts (as part of the Survey of Economic Projections) of the various FOMC participants, are other ways nontraditional policy is being implemented. These actions are intended to guide market expectations of the future short-term rate path.
Absent these unconventional policies, our model would likely have been conditioned on more adverse economic outcomes—specifically, a higher long-term interest rate and the related undesirable effects on unemployment and real output growth—which would have forced the fed funds rate to be even more negative. That said, our model analysis does not attempt to calculate the effect of those policies.
Conclusion
Using a particular class of statistical model, we have estimated the path of the federal funds rate had it not been constrained by zero lower bound. We show that the magnitude and persistence of adverse shocks experienced in the recent financial crisis would have forced the federal funds rate significantly below zero in this model. The model’s forecast suggests that the inability of the nominal federal funds rate to fall below zero was a binding constraint on the typical policy response in the path of the federal funds rate in this model. Policy makers employed unconventional methods to mitigate the restraint imposed by the zero lower bound by using quantitative easing stimulus. Some researchers estimate that these actions were equivalent to driving the federal funds rate to as low as negative 3 percent, but those findings are debatable.8 In sum, we suggest that the zero lower bound was binding to a great extent.
Footnotes
- See Rudebusch (2009, 2010) for examples of analysis similar to this commentary and using a Taylor rule reaction function for the Federal Reserve. Return to 1
- See Litterman (1980), Doan, Litterman, and Sims (1984), B, Giannoni, and Rechlin (2010), and Robertson and Tallman (1999). Return to 2
- As described below, the identification of the BVAR also includes the contemporary values of the model variables that precede it in the recursive ordering. Please refer to the third paragraph of the section called Underlying Sources Driving Federal Funds Rate Path for a discussion of the characteristics of a recursive ordering as an identification strategy. Return to 3
- We employ standard hyperparameter values for the prior restrictions applied to time series macroeconomic models as discussed in Beauchemin and Zaman (2011). Return to 4
- Taylor rule fed funds ratet = 2 + core inflationt
+ 0.5(core inflationt − 2)
+ 2(natural rate of unemploymentLR
− unemployment ratet). Return to 5 - We use a recursive ordering as the technique to identify the shocks and to decompose each variable’s forecast error into a function of all the uncorrelated shocks in the model. Table 1 lists the model variables in their order within the recursive structure. Real GDP is first in the structure, indicating that the variable responds to its own shock contemporaneously, but it does not respond contemporaneously to any other shock (but it responds to all uncorrelated shocks with a lag, as do all variables in the model). One can follow the logic to the final variable in the model (the trade-weighted nominal exchange rate), which responds to all uncorrelated shocks in the model contemporaneously (including its own). Return to 6
- Note that the sum of all the 17 shocks (including the fed funds rate shock) with the unconditional forecast of the federal funds rate (blue line) produces the actual data line. Return to 7
- See Chung, Laforte, Reifschneider, and Williams (2011), Bauer and Rudebusch (2011), Alon and Swanson (2011), and Gagnon, et al. (2011). Return to 8
References
- “The Fed’s Monetary Policy Response to the Current Crisis,” Glenn D. Rudebusch, 2009. Federal Reserve Bank of San Francisco, Economic Letter, no. 2009-17.
- “The Fed’s Exit Strategy for Monetary Policy,” Glenn D. Rudebusch, 2010. Federal Reserve Bank of San Francisco, Economic Letter, no. 2010-18.
- “Large-Scale Asset Purchases by the Federal Reserve: Did They Work?” Joseph Gagnon, Matthew Raskin, Julie Remache, and Brian Sack, 2010. Federal Reserve Bank of New York, Staff Report no. 441.
- “Have We Underestimated the Likelihood and Severity of Zero Lower Bound Events?” Hess Chung, Jean-Philippe Laforte, David Reifschneider, and John C. Williams, 2011. Federal Reserve Bank of San Francisco, working paper no. 2011-01.
- “Signals from Unconventional Monetary Policy,” Michael Bauer and Glenn Rudebusch, 2011. Federal Reserve Bank of San Francisco, Economic Letter, no. 2011-36.
- “The Effectiveness of Alternative Monetary Policy Tools in a Zero Lower Bound Environment,” James Hamilton and Jing (Cynthia) Wu, 2011. Unpublished manuscript, University of California, San Diego.
- “Operation Twist and the Effect of Large-Scale Asset Purchases,” Titan Alon and Eric Swanson, 2011. Federal Reserve Bank of San Francisco, Economic Letter, no. 2011-13.
- “A Medium Scale Forecasting Model for Monetary Policy,” Kenneth Beauchemin, and Saeed Zaman, 2011. Federal Reserve Bank of Cleveland, working paper no. 11-28.
- “Large Bayesian Vector Autoregressions,” Marta Banbura, Domenico Giannone, and Lucrezia Reichlin, 2010. Journal of Applied Econometrics, 25(1), 71-92.
- “Vector Autoregressions: Forecasting and Reality,” John C. Robertson and Ellis W. Tallman, 1999. Federal Reserve Bank of Atlanta, Economic Review, (Q1), 4-18.
- “Forecasting and Conditional Projection Using Realistic Prior Distributions,” Thomas Doan, Robert B. Litterman, and Christopher A. Sims, 1984. Econometric Reviews, 3, 1-100.
- “A Bayesian Procedure for Forecasting with Vector Autoregression,” Robert B. Litterman, 1980. Massachusetts Institute of Technology, Department of Economics, working paper.
- “A Historical Analysis of Monetary Policy Rules,” John Taylor, 1999.
Suggested Citation
Tallman, Ellis W., and Saeed Zaman. 2012. “Where Would the Federal Funds Rate Be, If It Could Be Negative?” Federal Reserve Bank of Cleveland, Economic Commentary 2012-15. https://doi.org/10.26509/frbc-ec-201215
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International






