- Share
Changing Policy Rule Parameters Implied by the Median SEP Paths
This Commentary estimates the implied parameters of simple monetary policy rules using the median paths for the federal funds rate and other economic variables provided in the Federal Open Market Committee’s Summary of Economic Projections (SEP). The implied policy rule parameters appear to have changed over time, as the federal funds rate projections have become less responsive to the unemployment gap. This finding could reflect changes in policymakers’ preferences, uncertainty over other aspects of the policy rule, or limitations of estimating simple monetary policy rules from the median SEP paths.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
Each quarter, the Federal Open Market Committee (FOMC) releases a compilation of its participants’ forecasts in the Summary of Economic Projections (SEP). The SEP is closely watched for hints about the future path of monetary policy. Yet by construction, each participant’s projections for economic growth, the unemployment rate, and inflation are conditional on his or her view of appropriate monetary policy. This means that the individual paths for the federal funds rate in the SEP are not necessarily forecasts for what policy will do; rather, they are more closely aligned with what each participant believes policy should do.
Looking at the relationship between projections for the appropriate federal funds rate and economic outcomes can provide a sense of the monetary policy “reaction function”—a general description of how policy is likely to respond under a variety of conditions. Because forecasts change as economic shocks occur, the insights into the reaction function implied by the SEP are arguably one of its strengths, even if these insights are imprecise; see Bernanke (2016). In this Commentary, I provide estimates of the reaction function in the SEP under the assumption that it takes the form of a particular simple monetary policy rule, which connects the federal funds rate to a small set of variables. To estimate the parameters of the implied simple policy rule, I relate the median path of the federal funds rate to the median projections for inflation and the unemployment rate, as a way to capture the center of the Committee.
Based on all of the SEPs available between December 2015 and March 2019, the parameters of the estimated policy rule bear some similarities to those in the original Taylor (1993) rule, after controlling for interest rate smoothing. When looking at each of the quarterly SEPs one at a time, however, the implied policy rule parameters appear to have changed over time. In particular, estimates suggest that the federal funds rate path has become less responsive to the unemployment gap over the last year; projections of the unemployment rate running below its longer-run level now put less upward pressure on the federal funds rate than was true earlier in the estimation sample. While this finding may reflect changes in policymakers’ preferences, it could alternatively or additionally reflect uncertainty over other aspects of the assumed simple policy rule, risk management considerations, or limitations of estimating simple monetary policy rules from the median SEP paths.
Simple Policy Rules and Interpolating the SEP
To quantify the reaction function implied by the SEP, I rely on simple monetary policy rules. Simple monetary policy rules serve as useful rules of thumb by positing that the monetary policy rate is a function of a small number of economic variables.1 Guided by this literature and the variables available in the SEP, the specific form of the simple policy rule that I consider is given by:
(1) it = ρit−1 + (1 — ρ)[r* + πt + α(πt − π*) + β(Ut − U*)] + εt.
The monetary policy rate in period t is given by it. The inflation gap is the difference between inflation, πt, and the inflation target, π*. Policy rules often have an activity gap that captures how far the economy is from potential; in this case, I use the unemployment gap, which is the difference between the unemployment rate, Ut, and the natural rate of unemployment, U*. The equilibrium real interest rate is r*. The parameter ρ captures the amount of inertia in the policy rule, α determines the responsiveness of policy to the inflation gap, and β determines the responsiveness of policy to the unemployment gap. Because I will be estimating the parameters of the policy rule, εt is the regression residual.
To line up the simple policy rule specified in equation (1) with the SEP, I make a number of important assumptions.2 First and foremost, I focus on the median projections for all variables. Considerable attention and news coverage focus on the median paths as the most salient information coming from the SEP, even though the SEP also contains the central tendency and the range of projections.3 However, this assumption is not innocuous, and I return to discuss it further below.
Second, I use the unemployment gap as my measure of economic activity rather than the output gap because the latter is not part of the SEP. The SEP reports the quarterly average unemployment rate in the fourth quarter of each year for the current year and the next two or three years. It also reports a median longer-run unemployment rate, which I assume is the estimate of the natural rate of unemployment (U*) throughout the forecast horizon for that particular SEP. Thus, I define the unemployment gap as the quarterly average of the unemployment rate minus the median longer-run unemployment rate.
Third, the target inflation rate π* is set to 2 percent, based on the FOMC’s Statement on Longer-Run Goals and Monetary Policy Strategy. This target value was first adopted in 2012 and has not changed. While the target is formally defined in terms of the annual change in the price index for personal consumption expenditures (PCE inflation), to abstract from high-frequency fluctuations in energy prices I calculate the inflation gap based on the difference between trailing four-quarter core PCE inflation, πt, which excludes food and energy prices, and the 2 percent objective.4
Fourth, the projections for the federal funds rates in the SEP are reported as the midpoint of the appropriate target range for the federal funds rate or the level of the appropriate federal funds rate at the end of each calendar year. To conform to this convention, the federal funds rates it and it−1 that enter equation (1) are the target funds rate values at the ends of period t and t−1, respectively, rather than the quarterly averages for the effective federal funds rate as is common in some studies.5 The equilibrium real federal funds rate r* is calculated as the median longer-run (nominal) federal funds rate minus the 2 percent inflation objective.
Fifth, the SEP reports projections for the average unemployment rate in the fourth quarter, the trailing four-quarter core PCE inflation rate in the fourth quarter, and the federal funds rate target at the end of the fourth quarter for the current year and the following two or three years. Because it is unclear from the SEP how long it will take to converge to the longer run and how that process will evolve, my analysis ends at either the two- or three-year-ahead horizon, which I will call year T.
Finally, policy rules of the form of equation (1) are usually estimated based on quarterly data. To do this estimation, I combine nowcasts for the current quarter of each SEP with the projections for the fourth quarter of each year up through year T and then linearly interpolate missing observations. For the current quarter, the nowcasts for core PCE inflation come from the four-quarter inflation rates implied by real-time core PCE data through the previous quarter and the real-time estimates of current-quarter inflation from the inflation nowcasting model on the Cleveland Fed’s website as of the first day of each FOMC meeting with an SEP submission.6 For the unemployment rate, I augment the real-time data on the first two monthly unemployment rate readings of the quarter that were available as of the first day of each meeting with an SEP submission with the trailing 3-month moving average to fill in the missing month and then take the quarterly average.7 For the current quarter and the previous quarter’s funds rate, I use the midpoints of the target ranges set by the FOMC.8
My estimation sample starts with the nowcasts and (interpolated) SEP forecasts from the December 2015 meeting, when the FOMC initially increased the federal funds rate target range after a long period in which the target range was held at 0 to 25 basis points. It ends with the nowcasts and (interpolated) SEP forecasts from the March 2019 meeting.
Estimation Results
In my first exercise, I pool all the nowcast and (interpolated) forecast observations into a single sample and estimate the implied parameters ρ, α, and β of the simple policy rule given by equation (1).9 In essence, this exercise assumes that the parameters of the implicit simple policy rule that explains the median federal funds rate path have been unchanged over the period from December 2015 through March 2019. The first two rows in table 1 report these results. The point estimates show considerable interest rate smoothing (ρ=0.88), a positive response to the inflation gap (α=1.01), and a negative response to the unemployment gap (β=−1.06).
| ρ | α | β | |
|---|---|---|---|
| 1. Whole sample | 0.88*** | 1.01*** | −1.06*** |
| 2. (Standard errors) | (0.01) | (0.34) | (0.13) |
| Estimation based on: | |||
| 3. 2015:Q4 | 0.81*** | 2.02** | −1.38 |
| 4. 2016:Q1 | 0.94*** | 0.12 | −14.89 |
| 5. 2016:Q2 | … | … | … |
| 6. 2016:Q3 | 0.83*** | 4.59*** | −0.78 |
| 7. 2016:Q4 | 0.92*** | 1.72 | −4.65 |
| 8. 2017:Q1 | … | … | … |
| 9: 2017:Q2 | … | … | … |
| 10. 2017:Q3 | 0.71*** | 1.35*** | −0.36 |
| 11. 2017:Q4 | 0.94*** | −2.73 | −2.67** |
| 12. 2018:Q1 | 0.93*** | −2.18 | −2.45 |
| 13. 2018:Q2 | 0.74*** | 2.48** | −0.27 |
| 14. 2018:Q3 | 0.67*** | 5.29*** | 0.23 |
| 15. 2018:Q4 | 0.79*** | −0.59 | −0.58*** |
| 16. 2019:Q1 | 0.88*** | 2.64 | 0.03 |
| Estimation based on: | |||
| 17. 2015:Q4–2018:Q1 | 0.89*** | 1.00** | −1.84*** |
| 18. (Standard errors) | (0.01) | (0.39) | (0.25) |
| 19. 2018:Q2–2019:Q1 | 0.82*** | 0.78 | −0.49*** |
| 20. (Standard errors) | (0.02) | (0.68) | (0.10) |
Notes: … indicates that parameter estimates are not available. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
Sources: Federal Reserve Board of Governors and author’s calculations.
To provide some context, consider two well-known simple policy rules: the Taylor (1993) rule and the Taylor (1999) rule. In their original formulations, these rules used the output gap instead of the unemployment gap. They also omitted interest-rate smoothing. If I use Okun’s law with an inverse Okun’s coefficient of −2.0 to translate the original formulations to comparable rules that use the unemployment gap instead of the output gap, and I allow for an arbitrary equilibrium real rate r*, the Taylor (1993) rule would be:10
(2) it = r* + πt + 0.5(πt − π*) − 1.0(Ut − U*),
while the Taylor (1999) rule would be:
(3) it = r* + πt + 0.5(πt − π*) − 2.0(Ut − U*).
After controlling for interest-rate smoothing and accounting for estimation uncertainty, the estimated coefficients on the unemployment gap and the inflation gap are not very different from those in the Taylor (1993) rule from equation (2).
While the first exercise assumes that the parameters of the implicit simple policy rule have been stable over the different SEPs, lines 3–16 of table 1 show the results from repeatedly estimating the parameters of the simple policy rule for each quarterly SEP, rather than assuming the parameters have been unchanged across SEPs. While this second exercise faces a number of limitations, it nevertheless reveals substantial heterogeneity in the implied policy rule parameters behind each SEP’s median federal funds rate path.11 Interestingly, the four coefficients on the unemployment gap are small in absolute terms for the SEPs from 2018:Q2 through 2019:Q1 compared with their earlier values.
In a third exercise, I use this perceived change in the coefficient estimates on the unemployment gap to divide the SEPs into two groups, and I reestimate the parameters over two samples: the SEPs from 2015:Q4 through 2018:Q1, and those from 2018:Q2 through 2019:Q1. The results are in lines 17–20 of table 1. The coefficients on the inflation gap and the unemployment gap in the early sample bear more similarities to those from the Taylor (1999) rule in equation (3) after controlling for interest-rate smoothing, as the coefficient on the unemployment gap is nearly double its full-sample estimate. By contrast, the coefficient on the unemployment gap is much smaller in the later sample—about half of the value in the Taylor (1993) rule—indicating that the median federal funds rate path recently has been less responsive to the unemployment gap than it had been. After accounting for estimation uncertainty, the coefficient on the inflation gap, meanwhile, appears to be little changed.
What Can Explain the Change?
There are a number of potential explanations for the change in the coefficient on the unemployment gap implied by the simple policy rules I consider. On the one hand, this change could reflect a true shift in preferences among policymakers. A smaller value of β in absolute terms means that the federal funds rate would respond less to deviations of the unemployment rate from its natural rate. Over time, the unemployment gap as calculated from the SEP medians has become more negative, implying a larger undershoot of the longer-run natural rate, as shown in figure 1. The reduced responsiveness of the funds rate to these unemployment gap projections could reflect a new asymmetry in the policy rule to large negative unemployment gaps, but testing this asymmetry would require seeing the policy response when the unemployment rate is above the natural rate as well.
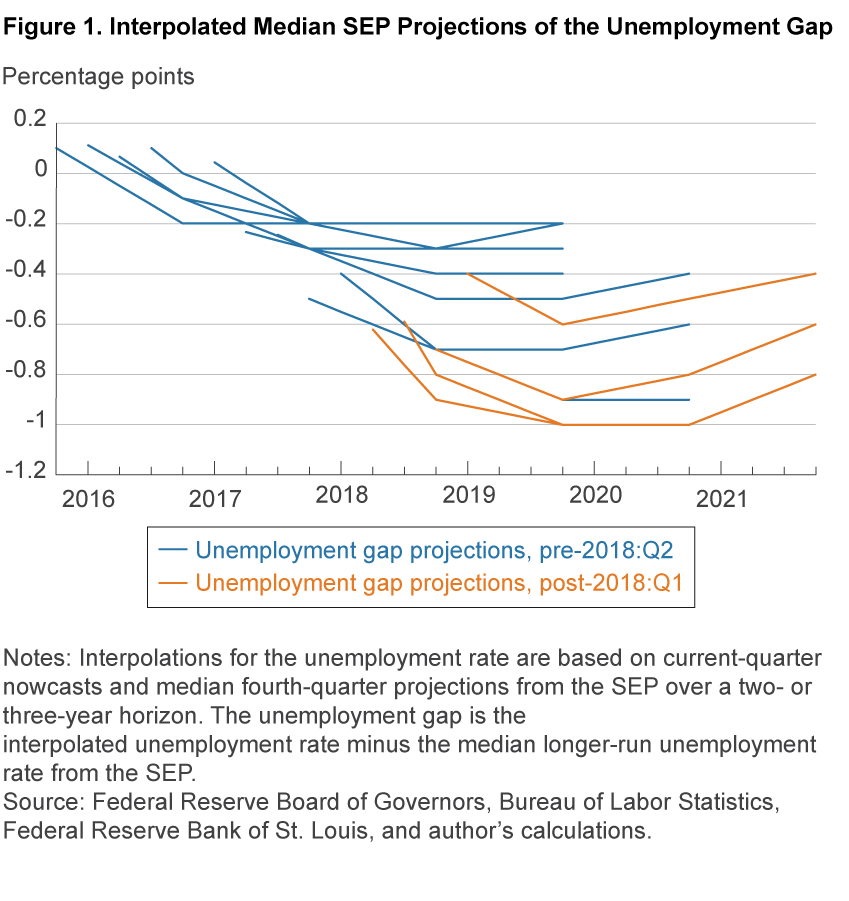
Alternatively, the change in this coefficient could reflect a preference to put less weight on the unemployment gap due to measurement challenges.12 Over time, the dispersion among FOMC participants’ forecasts for the longer-run unemployment rate has declined: In December 2015, there was a 1.1 percentage point difference between the highest and lowest longer-run unemployment rate projections, whereas in March 2019 the difference was only 0.6 percentage points. However, forecast dispersion is not equivalent to forecast uncertainty.13 It is possible that uncertainty over U* per se has been rising over time, including recently as inflation has failed to pick up despite ongoing declines in the unemployment rate relative to estimates of U*. The reduced weight on the unemployment gap in the implied policy rule may be an application of Brainard’s principle toward a concept that is subject to considerable uncertainty.14
Another related explanation is that the simple monetary policy rule proposed in equation (1) is an imperfect descriptor of monetary policy, and signals coming from other economic variables outside of the rule or risk management considerations over the last year have suggested that the appropriate path of policy should be different from what that particular rule would propose. Even though simple policy rules often serve as useful benchmarks, there are a large number of potential simple policy rules (see, e.g., Knotek et al. 2016), and there is no agreement on a single “best” rule under all economic circumstances (see, e.g., Mester 2016). In the case of the above findings, the decline in the estimated responsiveness of the federal funds rate toward the unemployment gap could be largely undone by other data suggesting that the broader labor market is not as tight as the unemployment gap would suggest.
To illustrate this possibility, figure 2 plots the interpolated March 2019 median federal funds rate path from the SEP along with two alternatives, both of which rely on the median SEP paths for core PCE inflation and the unemployment rate and start with the funds rate at its 2018:Q4 end-of-period value. The first alternative is generated by the policy rule estimated in table 1 based on the SEP values during the early period 2015:Q4–2018:Q1, with α=1.00, β=−1.84, and ρ=0.89, and the median longer-run values of U* and r* from the March 2019 SEP. This alternative path is markedly above the March SEP path, because the negative unemployment gap puts considerable upward pressure on the federal funds rate via the policy rule, which resembles an inertial Taylor (1999) rule. In the second alternative, the parameters of the policy rule are the same as those in the first alternative, but I lower the value of U* in the simulation from 4.3 percent (based on the SEP) to 3.75 percent. Without taking a stand on the plausibility of this estimate—which is below the range of FOMC participants’ longer-run estimates—this lower value for U* is intended to capture an “effective” unemployment gap potentially informed by other data suggesting that the labor market may not be as tight as would be implied by the unemployment gap. With the “effective” unemployment gap closed in this alternative, the policy path now closely resembles the median SEP path through the end of 2021. This is true even though the coefficient on the “effective” unemployment gap is set equal to its larger, pre-2018:Q2 level.
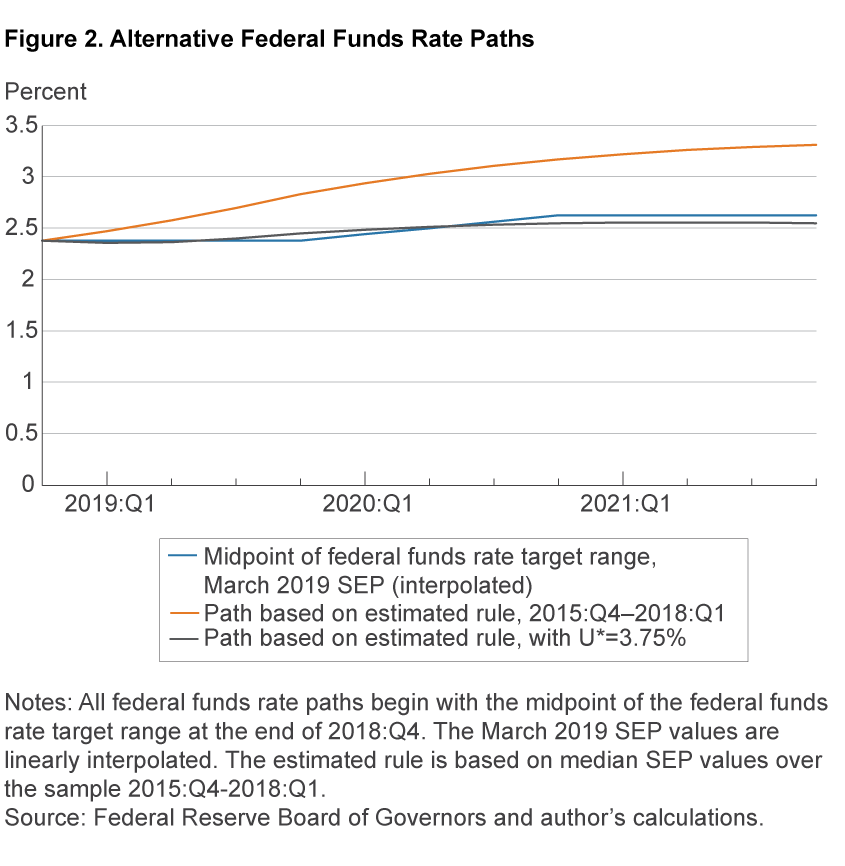
At the other extreme from documenting a true change in the responsiveness of the federal funds rate to the unemployment gap, it is possible that this finding could be spurious and reflects a limitation of using the median paths in the SEP for the analysis. As has been discussed in the past (e.g., Bernanke 2016), the median SEP path is not a consensus forecast of the FOMC. Each FOMC participant’s individual projection in the SEP is based on his or her most likely scenario of how the economy will unfold under his or her view of the appropriate path of monetary policy; see, e.g., Board of Governors of the Federal Reserve System (2019). Because the median values are constructed on a variable-by-variable basis at each point over the forecast horizon, there is no guarantee that they necessarily represent a coherent forecast of how policy would respond to economic developments.15
Conclusion
This Commentary estimates the implied parameters of a simple monetary policy rule using forecasts from the median paths of the variables in the SEP. It provides evidence that the median federal funds rate path has become less responsive to the median unemployment gap over the last year compared with the responsiveness that was implied by the median federal funds rate path earlier in the estimation sample. A number of alternative explanations can account for this finding, reflecting changes in policymakers’ preferences, uncertainty over other aspects of the policy rule, or limitations of estimating simple monetary policy rules from the median SEP paths.
Footnotes
- There is a vast literature on simple monetary policy rules; see, e.g., Taylor and Williams (2011), Knotek et al. (2016), or the simple monetary policy rules resources on the Cleveland Fed’s website for a brief introduction. Return to 1
- For other research estimating simple policy rules based on the SEP, see, e.g., Kahn and Palmer (2016). Return to 2
- For one example, Lahart (2019) provides the following description of the policy path from the March 2019 SEP: “Whereas in December their median projection called for two rate increases, now they expect none and next year they think they will raise rates only once.” Beyond the median, central tendency, and range of projections that are released immediately following FOMC meetings, the minutes of meetings associated with SEP releases also contain figures plotting the uncertainty surrounding the median paths of the projected variables based on historical forecast errors. Return to 3
- Bernanke (2015) provides one perspective on the inclusion of core PCE inflation in simple monetary policy rules of the form in equation (1). Qualitatively, the results are unchanged if I used headline PCE inflation from the SEPs instead of core PCE inflation. Return to 4
- The FOMC typically sets the target for the federal funds rate using multiples of one-quarter percentage point. This “discreteness” is discussed in Dueker (2002) and Dueker and Rasche (2004) and can affect quarterly averages of the federal funds rate target; quarterly averages of the effective federal funds rate are impacted by this discreteness along with variation in the effective rate relative to the target or midpoint of the target range. Taking into account this discreteness in the present study is further complicated by the fact that the median federal funds rate path sometimes ends in 1/8, 3/8, 5/8, or 7/8 of a percentage point, reflecting the midpoint of a target range, while in some cases it ends in 00, 25, 50, or 75 basis points, reflecting a point target rather than a range. To avoid taking a stand on when policy would change from targeting a range to a point, I omit the issue of discreteness in my baseline results. In results not reported, I enforced discreteness by assuming that the federal funds rate path would always be at the midpoint of a target range and would end in 1/8, 3/8, 5/8, or 7/8 of a percentage point; e.g., once the interpolated federal funds rate was in the range of [1.50%, 1.75%), the funds rate would take on the value 1-5/8 percent. The results from this exercise were qualitatively and quantitatively similar to those presented herein. Return to 5
- Knotek and Zaman (2017) document that the current-quarter core PCE inflation nowcasts from this model have historically been quite accurate, and their nowcasting performance has been historically similar to the accuracy of the Board staff’s projections as captured in the Greenbook. Core PCE data come from the Bureau of Economic Analysis, with real-time vintages from the St. Louis Fed’s Archival Economic Data (ALFRED) database. Return to 6
- For the fourth quarter of each year, I use the median SEP values for the current-quarter unemployment rate and current-quarter trailing four-quarter core PCE inflation. The real-time unemployment rate data come from the Bureau of Labor Statistics via ALFRED. Federal funds rate targets are from the statements of the FOMC via the Board of Governors website. Return to 7
- I focus exclusively on SEP projections and hence on the associated meetings. Focusing on policy decisions as of the meetings with an SEP submission conforms to the recent pattern in which changes in the policy rate have only occurred at SEP-associated meetings. Return to 8
- To impose the coefficient restrictions from equation (1), the parameters are estimated by nonlinear least squares. For each SEP, there is a single U* and a single r*, which I assume enter the policy rule for all the observations associated with that SEP, but the values of U* and r* can and have changed over time. This exercise allows for this time variation in U* and r* across SEPs. Return to 9
- Okun’s law (Okun 1962) posits that there is a negative relationship between the output gap and the unemployment gap. Yellen (2012) uses a value of −2.3 for the inverse of Okun’s coefficient to translate output gaps into unemployment gaps when working with the Taylor (1993) and Taylor (1999) rules. Taking into account time variation in Okun’s coefficient as documented in Knotek (2007) gives a value of −1.3 as of the first quarter of 2019 for the inverse of Okun’s coefficient, as reported in the spreadsheet accompanying the Cleveland Fed’s simple monetary policy rules page. A value of −2.0 appears reasonable for this rule of thumb. Return to 10
- In particular, estimation is conducted based on a small number of quarterly observations for each SEP, ranging from 11 to 14, and standard errors are often large. In some cases, there is not enough variation in the forecasts to estimate the implied policy rule parameters, as indicated in the table. In addition, in some cases the estimates are highly sensitive to the assumed current-quarter values, because there are few data points and the initial values can affect several subsequent observations due to linear interpolation. Partly as a result, and partly in the interests of space, I omit standard errors from the table. Return to 11
- In one well-known estimate, Staiger et al. (1997) estimated the width of the 95 percent confidence interval for the nonaccelerating-inflation rate of unemployment to be approximately 3 percentage points wide; see Council of Economic Advisers (2016) for even wider recent estimates using the same technique. Return to 12
- For some recent research that comes to a similar conclusion, see, e.g., Rich and Tracy (2018). Return to 13
- See, e.g., Blinder (1998) for more on the Brainard principle as applied in central banking. Powell (2018) discusses navigating monetary policy by the “stars,” one of which is U*. Return to 14
- Faust (2016) provides further discussion on the limitations of the SEP. Return to 15
References
- Bernanke, Ben S. 2015. “The Taylor Rule: A Benchmark for Monetary Policy?” Brookings blog (April 28, 2015; accessed April 8, 2019).
- Bernanke, Ben S. 2016. “Federal Reserve Economic Projections: What Are They Good For?” Brookings blog (November 28, 2016; accessed April 8, 2019).
- Blinder, Alan S. 1998. Central Banking in Theory and Practice, Cambridge, MA: MIT Press.
- Board of Governors of the Federal Reserve System. 2019. “Transcript of Chair Powell’s Press Conference Opening Remarks.” (March 20, 2019).
- Council of Economic Advisers. 2016. Economic Report of the President, Together with the Annual Report of the Council of Economic Advisers (February).
- Dueker, Michael J. 2002. “The Monetary Policy Innovation Paradox in VARs: A ‘Discrete’ Explanation.” Federal Reserve Bank of St. Louis, Review, 84(2): 43–50.
- Dueker, Michael J., and Robert H. Rasche. 2004. “Discrete Policy Changes and Empirical Models of the Federal Funds Rate.” Federal Reserve Bank of St. Louis, Review, 86(6): 61–72.
- Faust, Jon. 2016. “Oh What a Tangled Web We Weave: Monetary Policy Transparency in Divisive Times.” Hutchins Center Working Paper No. 25 (November).
- Kahn, George A., and Andrew Palmer. 2016. “Monetary Policy at the Zero Lower Bound: Revelations from the FOMC’s Summary of Economic Projections.” Federal Reserve Bank of Kansas City, Economic Review (First Quarter): 5–37.
- Knotek, Edward S., II. 2007. “How Useful Is Okun’s Law?” Federal Reserve Bank of Kansas City, Economic Review, 92(4): 73–103.
- Knotek, Edward S., II, Randal J. Verbrugge, Christian Garciga, Caitlin Treanor, and Saeed Zaman. 2016. “Federal Funds Rates Based on Seven Simple Monetary Policy Rules.” Federal Reserve Bank of Cleveland, Economic Commentary, 2016-07.
- Knotek, Edward S., II, and Saeed Zaman. 2017. “Nowcasting US Headline and Core Inflation.” Journal of Money, Credit and Banking, 49(5): 931–968.
- Lahart, Justin. 2019. “Cautious Fed Decides to Play It Safe.” Wall Street Journal, March 21, 2019, B12.
- Mester, Loretta J. 2016. “A Monetary Policymaker’s Lexicon.” Speech given at Market News International, New York, New York (February 4, 2016).
- Okun, Arthur M. 1962. “Potential GNP: Its Measurement and Significance.” American Statistical Association, Proceedings of the Business and Economics Statistics Section, 98–104.
- Powell, Jerome H. 2018. “Monetary Policy in a Changing Economy.” Remarks delivered at “Changing Market Structure and Implications for Monetary Policy,” a symposium sponsored by the Federal Reserve Bank of Kansas City, Jackson Hole, Wyoming (August 24, 2018).
- Rich, Robert, and Joseph Tracy. 2018. “A Closer Look at the Behavior of Uncertainty and Disagreement: Micro Evidence from the Euro Area.” Federal Reserve Bank of Cleveland, Working Paper No. 18-13.
- Staiger, Douglas, James H. Stock, and Mark W. Watson. 1997. “The NAIRU, Unemployment and Monetary Policy.” Journal of Economic Perspectives, 11(1): 33–49.
- Taylor, John B. 1993. “Discretion versus Policy Rules in Practice.” Carnegie-Rochester Conference Series on Public Policy, 39: 195–214.
- Taylor, John B. 1999. “A Historical Analysis of Monetary Policy Rules.” In John B. Taylor, ed. Monetary Policy Rules, Chicago: University of Chicago Press, 319–348.
- Taylor, John B. and John C. Williams. 2011. “Simple and Robust Rules for Monetary Policy.” In Benjamin M. Friedman and Michael Woodford, eds., Handbook of Monetary Economics, vol. 3B, San Diego: North Holland, 829–860.
- Yellen, Janet L. 2012. “The Economic Outlook and Monetary Policy.” Remarks at the Money Marketeers of New York University, New York, New York (April 11, 2012).
Suggested Citation
Knotek, Edward S., II. 2019. “Changing Policy Rule Parameters Implied by the Median SEP Paths.” Federal Reserve Bank of Cleveland, Economic Commentary 2019-06. https://doi.org/10.26509/frbc-ec-201906
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International





