- Share
Using an Improved Taylor Rule to Predict When Policy Changes Will Occur
A standard Taylor rule, which expresses the federal funds rate as a function of inflation, the unemployment gap, and the past federal funds rate, tracks the federal funds rate well over time. We improve the fit by adding employment growth. Then we evaluate the effectiveness of that rule in a new way—by how accurately it predicts whether the FOMC moves the fed funds rate at its next meeting. It does pretty well, predicting nearly 70 percent of the time correctly.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
The Federal Reserve's Federal Open Market Committee (FOMC) meets regularly throughout the year to set monetary policy. In "normal times," the FOMC conducts policy by targeting the federal funds rate, the interest rate at which banks borrow funds from each other overnight. This rate has fallen to practically zero since the financial crisis, and the FOMC has indicated that the rate will likely be there for a considerable time. But eventually, "normal times" will return, and the FOMC will increase the rate. When that happens, there will be renewed interest in predicting where the fed funds rate will be in the future.
Often, the FOMC's adjustments to the fed funds rate target are thought of in terms of a Taylor rule. First posited in 1993 by the economist John Taylor, the rule is an equation that expresses the fed funds rate in terms of at least two important economic indicators, the rate of inflation and the gap between the economy's current performance and its full potential. The gap is measured in different ways, and other variables are often added to the rule to better approximate the actual behavior of the fed funds rate. The most important is the recent past level of the federal funds rate, which has the effect of reducing the size of the target and reflects the presumption that the Fed does not like large changes in its target rate.
A Taylor rule with these variables tracks the funds rate well over time. But we have found that the fit is improved if we include not only current unemployment but also the direction that unemployment is likely heading, which we proxy for by also adding employment growth to the rule. Adding employment growth improves the fit substantially, and the improvement is especially large during recessions.
We also describe a new way to evaluate the performance of the Taylor rule. While the accuracy of a Taylor rule is typically measured by how far the actual funds rate is from the rule's prediction, it might also be measured by how often if predicts whether the target rate will be changed at the next FOMC meeting. We present a way to use the rule to make this prediction and evaluate its performance.
Improving the rule's accuracy can help both policymakers and the public. Of course, the Fed does not respond mechanically to any such rule, but the Taylor rule can provide a useful guidepost. It captures the behavior of past policy and can quickly show policymakers the target rate that the past approach would suggest in current circumstances. To the extent that policymakers think past policy was in general successful, the Taylor rule might therefore guide them going forward. Outside of the FOMC, people can use the rule to help anticipate future changes in the target.
Employment in the Taylor Rule
At its heart, the Taylor rule estimates a target for the fed funds rate that will move inflation and economic performance toward desired levels. The original rule expressed the target as a function of the deviation of actual inflation from the FOMC's goal and the gap between current and potential levels of GDP. Unemployment is often used in place of GDP, since it also reflects economic performance but corresponds more closely to the Fed's mandate. This is the version we use in thisCommentary.
The interpretation of a Taylor rule with unemployment is as follows. The funds rate target estimated by the rule should equal some long-run equilibrium level plus adjustments meant to correct for deviations in actual inflation and unemployment from the FOMC's long-run goals for each variable. The long-run level of the funds rate is the sum of the FOMC's inflation goal and the long-run real rate of interest (the rate of interest at which inflation and unemployment are at the FOMC's long-run goals). So, for example, if the inflation goal is 2 percent and the long-run real rate of interest is 2 percent, the long-run level of the funds rate would be 4 percent. (Note that this long-run level is expressed in nominal terms, so it is unadjusted for inflation.)
As for deviations from the long-run goals, the rule requires adjustments to the fed funds rate when the current rate of inflation deviates from the FOMC's specified goal (currently 2 percent) and the unemployment rate deviates from some measure of the NAIRU. (NAIRU stands for nonaccelerating inflation rate of unemployment and refers to a level of the unemployment rate below which inflation rises.)
In addition, our rule includes the past funds rate to reflect the fact that the funds rate moves slowly over time, and that the FOMC moves slowly toward a medium-term target. The predicted fed funds rate in this type of rule is the weighted sum of the past fed funds rate and the medium-run target, which is the fed funds rate that is implied by the standard Taylor rule. (Note that the medium-term target can change from quarter to quarter, since the economic factors that enter the rule - inflation and unemployment - can change from quarter to quarter.) The weight assigned to the past funds rate is denotedthe persistent or inertial factor, and the weight assigned to the medium-term or standard Taylor-rule part of the rule is denotedthe partial adjustment factor. The rule itself is called a partial-adjustment Taylor rule.
The unemployment Taylor rule with partial adjustment is estimated by regressing the funds rate on the lagged funds rate, the unemployment gap (the unemployment rate minus the NAIRU), and inflation.1
To this version of the rule, we add employment growth. This variable allows us to capture the change in the pace of real economic activity. The following metaphor may explain why it improves the rule's accuracy. Think of the FOMC setting the target fed funds rate as the captain who is guiding a ship to the dock. The decision to increase or decrease the engine speed (interest rates) is affected both by the ship's current location (unemployment rate) and its speed (employment growth).
Figure 1 presents our estimates from the two versions of the unemployment-based Taylor rule, one with only unemployment and one with unemployment plus employment growth. Both rules seem to track the broad tendencies in the behavior of the funds rate. But looks can be misleading. The unemployment-only rule essentially lags behind the actual funds rate changes by one quarter. (In figure 1 the blue line is shifted to the right of the gold line.) The average miss is 35 basis points (bp). To put that number in perspective, it is nearly the same level of accuracy as that of a purely naïve rule, where the funds rate is simply last quarter's funds rate and for which the average miss is 37 bp.
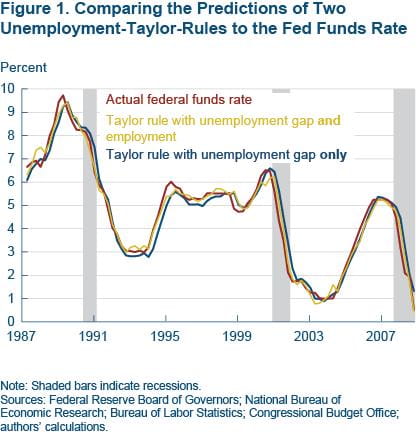
Notice that there are periods when the unemployment-only rule can miss quite substantially. For example, in 2001:Q2 it missed by a whopping 130 bp. The rule with both unemployment and employment growth does much better. The lagging pattern is not as prominent, and the 130 bp miss during the 2001 recession is reduced to 70 bp. The average miss now is 25 bp.
But as figure 2 makes apparent, the employment-growth rule looks especially helpful during recessions.
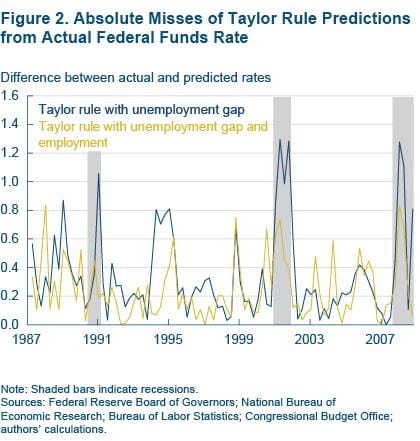
In fact, the rule with employment growth delivers a 39 basis point improvement in average misses during recessions over the rule with unemployment alone - 42 bp compared to 81 bp (table 1). By comparison, the average of the absolute value of the misses for the purely naïve rule is 89 bp.
Table 1. Sensitivity Analysis for Various Specifications of the Taylor Rule, 1987-2008
| Specification | Absolute misses (basis points) | Percent of moves predicted correctly | ||||
|---|---|---|---|---|---|---|
| Overall | Two quarters before recession | Recessions | Two quarters after recession | Non-recessions | ||
| Unemployment gap | 0.35 | 0.13 | 0.81 | 0.23 | 0.27 | 49 |
| Unemployment gap and employment growth | 0.25 | 0.30 | 0.42 | 0.15 | 0.22 | 67 |
| Unemployment gap and GDP growth | 0.28 | 0.25 | 0.45 | 0.25 | 0.26 | 64 |
| Naïve rule | 0.37 | 0.14 | 0.89 | 0.30 | 0.29 | 47 |
Source: Authors' calculations.
The rule with employment growth also does slightly better in the two quarters after a recession, with an 8 bp improvement over unemployment alone. On the other hand, the rule with employment growth does worse just before recessions, calling for relatively easier policy. On average it gives a fed funds rate that is 12 basis points below the actual fed funds rate in the two quarters before recessions begin.
Predicting Policy Moves
Thus far we have shown that the average miss from the actual funds rate is improved, especially during recessions, when a current measure of the change in the pace of economic activity, such as employment growth, is included in the Taylor rule. We next describe how to use this Taylor rule to develop a way of predicting when the funds rate will change on a quarter-by-quarter basis.
We start with the idea behind the partial-adjustment Taylor rule. Recall that partial-adjustment is added to the Taylor rule to reflect the assumption that the Fed heads slowly to its medium-range target over the course of the next several meetings rather than moving all at once. The rule can be thought of as consisting of a medium-run target for policy and a partial-adjustment factor, which is one minus the weight assigned to the past fed funds rate. With a small weight on last quarter's funds rate, the funds rate estimate moves very quickly to its medium-run target; with a large weight, the opposite occurs.
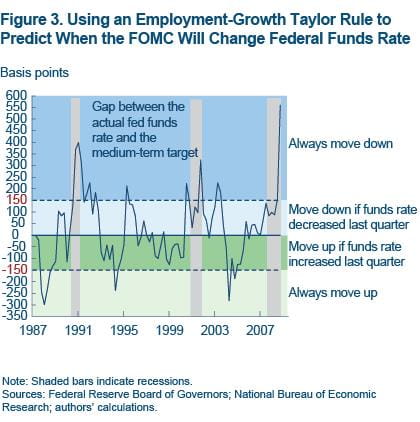
We use the partial adjustment factor to determine a threshold above or below which the FOMC will always move to its medium-run target. First we note that a typical adjustment rate in this type of Taylor rule is approximately 1/6, which means that the central bank moves the funds rate 1/6 of the way toward the medium-run target in every quarter. This fraction was determined empirically; it's the weight that gets the closest fit to the historical data. Then, we consider the fact that the smallest move the FOMC makes in a quarter is generally 25 bp. Together these observations imply, roughly speaking, that the FOMC is expected to move when the actual funds rate deviates from its medium-run target by at least 150 basis points (1/6 of 150 bp is 25 bp).
Using this 150 bp as the threshold, we look at the spread between the actual fed funds rate and the medium-run target quarter by quarter. If the spread exceeds 150 bp, we assume that policymakers will always move. We then assume that the FOMC will keep moving (decreasing the spread) until the gap is less than 25 bp.
When the actual funds rate is within 150 bp of the medium-run target, the situation is ambiguous. The FOMC might actively move to bring the funds rate closer to target, or it might take no action and allow the rate to move away from the target until the 150 bp threshold is again breached. To deal with this ambiguity, we look back to the previous quarter. If the actual funds rate was lowered or raised and it reduced the spread in that quarter, it indicates that the Fed moved to close the gap. We assume it will continue to do so in the current quarter, and another move will be in order. Figure 3 illustrates this scenario.
This approach predicts when moves occur, not the size of the move (it is assumed to be 25 bp). Using this rule, figure 4 plots actual moves against predicted moves. A plus one indicates a move up, minus one a move down, and zero no move. Even during some misses the rule was off by only a quarter or so. Looking at the chart shows there are two long time periods when the rule was off, before the latest recession and before the 2001 recession. In those cases, the rule called for easier monetary policy than was actual policy, which is consistent with what we found earlier. While looking back it might be easy to say that following the rule would have been preferable, 20-20 hindsight is never fair.
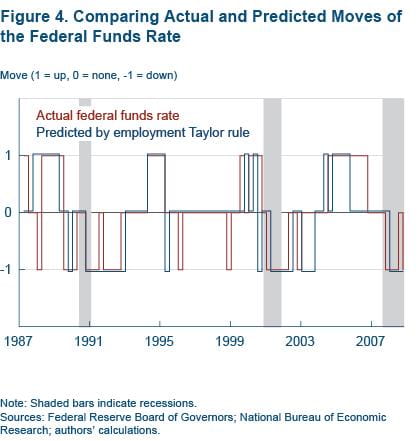
The last column of table 1 shows that the Taylor rule with both unemployment and employment growth correctly predicted when the funds rate would change, as well as its direction, 67 percent of the time. (With GDP growth instead of employment growth, the results are similar, 64 percent.) But with just unemployment, the percentage correct falls dramatically to 49 percent. In fact, the unemployment-only rule's predictive performance is again basically the same as the naïve rule's, 47 percent. (Recall that a naïve rule predicts that the funds rate this quarter will be the same as last quarter, in other words, that the FOMC never moves.)
In Practice
While a standard Taylor rule with unemployment broadly tracks the federal funds rate, because it is based only on the current level of economic conditions, it provides limited guidance on a meeting-to-meeting basis. Adding current indicators like employment growth or GDP growth to the rule substantially improves the overall fit, especially during recessions, because they capture the changing pace of real economic activity. Both of these indicators offer about the same degree of improvement in fit, although employment growth slightly outdoes GDP growth. From a practical standpoint, however, employment growth might make more sense because it comes out monthly, whereas GDP comes out quarterly.
The rule of thumb we developed predicts when the FOMC historically might have changed policy. It is most accurate when it uses a version of the Taylor rule with employment growth. It then correctly predicts policy actions 67 percent of the time, a substantial improvement over the version with just unemployment, when it predicts correctly only 49 percent of the time. This 18 percentage point improvement is quite substantial, especially when one considers that the unemployment-only Taylor rule improves upon the purely naïve rule by just 2 percentage points.
Footnotes
- NAIRU is defined by the CBO. For employment growth we use the quarterly growth rate of total nonfarm payroll employment. For real GDP growth we use annual growth rates instead of quarterly because they predict historical monetary policy better and because they smooth out inventory adjustments that may have unduly large effects on quarterly growth. We use real-time data for all the variables except inflation so that we mirror the data the Fed actually had available at the time of its policy decision. For inflation, we use core CPI instead of core PCE because the PCE is subject to more revision, and we used the revised core CPI inflation series since the real-time series does not go back far enough. Return to 1
Suggested Citation
Carlstrom, Charles T., and Saeed Zaman. 2014. “Using an Improved Taylor Rule to Predict When Policy Changes Will Occur.” Federal Reserve Bank of Cleveland, Economic Commentary 2014-02. https://doi.org/10.26509/frbc-ec-201402
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International





