- Share
Forecasting Inflation? Target the Middle
The Median CPI is well-known as an accurate predictor of future inflation. But it’s just one of many possible trimmed-mean inflation measures. Recent research compares these types of measures to see which tracks future inflation best. Not only does the Median CPI outperform other trims in predicting CPI inflation, it also does a better job of predicting PCE inflation, the FOMC’s preferred measure, than the core PCE.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
At the end of 2012, the Federal Open Market Committee (FOMC) adopted a new guideline for determining when it would consider raising interest rates. What is different about the guideline is that it gives specific thresholds for various economic indicators, which if reached, would signal a change in the Committee’s interest-rate target. These thresholds were spelled out in the meeting statement: “…the Committee…currently anticipates that this exceptionally low range for the federal funds rate will be appropriate at least as long as the unemployment rate remains above 6 1/2 percent, inflation between one and two years ahead is projected to be no more than a half percentage point above the Committee’s 2 percent longer-run goal, and longer-term inflation expectations continue to be well anchored.”
While the unemployment-rate threshold is expressed in terms of current conditions, the inflation threshold is in terms of the outlook for inflation. By specifying the inflation threshold in terms of its forecasted values, the FOMC will still be able to “look through” transitory price changes, like they did, for example, when energy prices spiked in 2008. At that time, the year-over-year growth rate in the Consumer Price Index (CPI) jumped up above 5.0 percent but subsequently plummeted below zero a year later when the bottom fell out on energy prices. At the time, the Committee maintained the federal funds rate target at 2.0 percent, choosing not to react to the energy price spike. Under the explicit inflation threshold, the Committee will not lose its ability to remain forward looking, and will rely on forecasts of inflation.
To help inform those inflation projections, Chairman Bernanke, in a recent press conference, stated that the Committee “will consider a variety of indicators, including measures such as median, trimmed mean, and core inflation; the views of outside forecasters; and the predictions of econometric and statistical models of inflation.” In this Economic Commentary, we highlight the usefulness of trimmed-mean measures (chiefly, the median CPI) in gauging the underlying inflation trend and forecasting future inflation.
Drilling Down to the “Core”
Perhaps the most well-known underlying inflation measure is the “core” Consumer Price Index (CPI).1 This measure excludes the prices of food and energy items because those were the two most volatile categories when the core CPI was conceived. While energy remains the most volatile broad category, food prices have become much less volatile in recent years.
Exclusionary measures have a couple of drawbacks. First, they always treat price changes in the categories they exclude as noise. This becomes a problem if there is information on inflationary pressures embedded in those excluded categories. More importantly, these measures always treat the price changes that they retain as an inflation signal. For example, if an excise-tax increase pushed up the retail price of tobacco, even though that has little to do with inflation, it would get included in the core CPI, hence overstating underlying inflation.
Fortunately, there are alternatives to the core CPI. One is trimmed-mean inflation statistics. These measures separate the inflation signal from relative-price noise by ignoring the most volatile monthly price swings. Calculating a trimmed-mean measure is relatively simple. The monthly price changes in the consumer market basket are ordered from lowest to highest price change, and the tails of the distribution are dropped. For example, the symmetric 16 percent trimmed-mean CPI cuts 8 percent (by expenditure weight) off of the low end and 8 percent from the high end of the price-change distribution. Then a weighted average is taken of what’s left over. And calculating the median CPI, which is just an extreme trimmed-mean measure, is even easier, in that it uses only the price change in the middle of the distribution.
There are a myriad of possible trimmed-mean inflation measures to choose from. Some are symmetric, in that they trim an equal amount from each tail, and some are asymmetric, in that they trim more from one tail than the other. But which trimmed mean should we pay attention to? And how confident should we be that the “best-performing” trimmed-mean measure over the past will remain so in the future?
Some recent work from the Cleveland Fed—Meyer and Venkatu (2012)—attempts to answer those questions by evaluating the full set of symmetric and asymmetric trims. They are chiefly interested to see if any particular trimmed-mean measure can track future inflation better than all the other trims.
Meyer and Venkatu find that the most accurate trimmed-mean CPI appears to vary across different sample periods. Over some time horizons, the inflation signal is strong enough that a less aggressive trimmed mean is sufficient (such as a 10 or 16 percent trimmed mean). However, over other time periods, a much more aggressive trimmed mean (like the median CPI) is necessary to separate relative-price noise from inflation signal.
This poses a potential problem, because in “real-time” we are never sure of how aggressive we need to be with the trimming procedure. One strategy to deal with this issue might be to always use the most aggressive trimmed mean—the median CPI. However, before we do that, we want to be sure that we’re not throwing away information that could be potentially useful in tracking underlying inflation.
What we really care about is whether a particular trimmed mean is giving us a meaningful difference in forecasting power. Even though the “optimal” trimmed-mean measure changes over time, if its performance is not materially different from, say the median CPI, we can be confident in the inflation signal that is coming from the median CPI.
This difference in forecasting power can be discerned using a simple statistical test. Testing the statistical significance of the most accurate trimmed-mean measure versus all others gives us an idea of how unique that performance is, in the sense that we will be able to visualize whether there is a tight grouping of equally performing trimmed means around the “best” trim, or whether there is a wide swath of trimmed-mean measures that have statistically similar forecasting performance. The results of this test are plotted in figure 1.
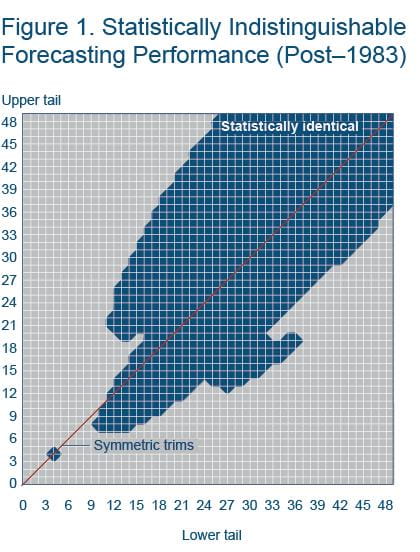
Figure 1 plots all the different possible trimming combinations, with the percent trimmed from the lower tail of the price-change distribution on the horizontal axis, and the percent trimmed from the upper tail on the vertical axis. The red line traces out the symmetric trimming points, from the zero-trim (headline) CPI in the lower left, to the median CPI in the upper right. The large swath in blue contains all the trims with the lowest forecast error and statistically similar forecasting accuracy.2
The huge swath of blue in figure 1 tells us, with 90 percent confidence, all the trimmed-mean measures contained within carry about the same forecasting accuracy as the most accurate trimmed-mean over that sample period. In other words, a 30 percent trimmed mean (one that cuts off 15 percent from each tail of the price-change distribution) carries about the same forecasting accuracy as the median CPI since 1983.
Interestingly, figure 1 also suggests that there is a penalty to asymmetrically trimming, as moving the trimming points too far toward the upper left-hand or lower right-hand corners results in a significant reduction in forecast accuracy. For example, trimming 40 percent off the lower tail of the price-change distribution and only 25 percent off the upper tail would result in a meaningful deterioration in performance.
So, which trimmed-mean measure should garner our attention? The recent study from the Cleveland Fed runs the test shown in figure 1 over multiple time periods. While the large swath of equally performing trimmed-means changes slightly between periods, the median CPI is always in that robust forecasting set.
A Simple Forecast
Any useful measure of underlying inflation should be able to quickly distinguish inflation signal from relative-price noise. Given this high signal-to-noise ratio, its near-term trend should be able to predict future inflation. Table 1 compares the forecasting accuracy, as measured in terms of root-mean-squared error (RMSE), of the near-to-longer term growth rates in the headline CPI, core CPI, and median CPI. A lower RMSE means a more accurate forecast, with a value of zero indicating perfect foresight. For example, taking the one-month annualized growth rate in the median CPI to forecast inflation over the next year yields a RMSE of 1.22, which is roughly 16 percent more accurate than the one-month percent change in the core CPI.
Table 1. Forecasting Accuracy For CPI Inflation over the Next One to Two Years
| 12 months ahead | 24 months ahead | ||||||
|---|---|---|---|---|---|---|---|
| Root-mean squared error (RMSE) | Root-mean squared error (RMSE) | ||||||
| Percent change last | CPI | Core CPI | Median CPI | Percent change last | CPI | Core CPI | Median CPI |
| 1 month | 3.28 | 1.67 | 1.46 | 1 month | 3.23 | 1.45 | 1.22 |
| 3 months | 2.59 | 1.44 | 1.37 | 3 months | 2.40 | 1.14 | 1.09 |
| 6 months | 2.09 | 1.38 | 1.34 | 6 months | 1.86 | 1.06 | 1.05 |
| 9 months | 1.83 | 1.37 | 1.33 | 9 months | 1.60 | 1.07 | 1.05 |
| 12 months | 1.70 | 1.37 | 1.33 | 12 months | 1.48 | 1.07 | 1.05 |
| 24 months | 1.49 | 1.37 | 1.33 | 24 months | 1.25 | 1.08 | 1.02 |
As is evident in the figure, the median CPI has a lower forecasting error than the core CPI, and both are much more accurate than the headline CPI. Also, it appears that the median CPI more quickly sheds relative-price noise, as the greatest difference between it and the core CPI is over the very near term (one- through three-month annualized growth rates). In this sense, the median is more likely to act as an early warning system in the event that inflation starts to pick up.
Forecasting PCE inflation
So far we’ve focused primarily on the CPI-based inflation measures, but the FOMC’s explicit inflation objective is expressed in terms of the Personal Consumption Expenditures (PCE) Price Index. There are significant differences between it and the CPI.3 However, inflation is a monetary impulse that affects prices in general, and over time, the inflation trend measured by the CPI and the PCE should be broadly similar.
More importantly, any appropriate underlying inflation measure ought to be able to tease out that inflationary impulse regardless of which measure of retail prices it is based on. In the forecasting exercise below, we show that the median CPI is, by that definition, an appropriate underlying inflation measure, as it is useful in forecasting headline PCE inflation. In fact, it can even be helpful in forecasting core PCE inflation.
Recent work by Meyer and Zaman (2013) evaluates the use of the median CPI in a class of statistical models known as Bayesian Vector Autoregressions (BVARs), which are often used for macroeconomic-policy forecasting. These statistical models efficiently estimate historical relationships between variables and use those correlations to forecast.
Table 2 illustrates the usefulness of the median CPI in forecasting PCE-based inflation. We highlight these gains in forecast accuracy in two different exercises using a medium-scale (18-variable) monthly BVAR model. First, we add the median CPI alongside the core PCE in the model and compare forecasts of core and headline PCE inflation from one-month to 24-months ahead. Then we run a similar exercise where we replace the core PCE with the median CPI as the underlying inflation measure in the model and forecast headline PCE inflation. The values shown in the table are the forecast errors of the model that makes use of the median CPI relative to the one without. A value below 1.0 indicates that the forecasting model that uses the median CPI is more accurate.
Table 2. Forecasting Accuracy in a More Complex Statistical Model
| Relative mean squared error | ||||||||
|---|---|---|---|---|---|---|---|---|
| BVAR with the median CPI added to the model | ||||||||
|
|
h=1M | h=6M | h=9M | h=12M | h=15M | h=18M | h=21M | h=24M |
| PCE | 0.962 | 0.974 | 0.979 | 0.957 | 0.970 | 0.955 | 0.956 | 0.954 |
| Core PCE | 0.968 | 0.966 | 0.961 | 0.967 | 0.939 | 0.909 | 0.905 | 0.893 |
| BVAR with the median CPI replacing the core PCE | ||||||||
|
|
h=1M | h=6M | h=9M | h=12M | h=15M | h=18M | h=21M | h=24M |
| PCE | 0.979 | 0.98 | 0.979 | 0.945 | 0.961 | 0.941 | 0.947 | 0.951 |
Notes: A value below 1.0 means the model with the median CPI is more accurate. Forecasting results from the Carriero, Clark, and Marcellino (2011) benchmark BVAR estimated recursively with an initial estimation period of January 1967 to December 1986. The forecast evaluation period begins in January 1987 and runs through 2011.
As both exercises indicate, making use of the median CPI (either alongside or in place of the core PCE) aids in forecasting inflation. In general these gains are modest, roughly 5 percent, on average. However, for core PCE, the improvement in forecasting accuracy hits about 10 percent at horizons of 18 months and beyond. This suggests that the median CPI is an appropriate measure of underlying inflation—one that can overcome the idiosyncrasies of the price index it’s based on and more completely uncover the inflationary impulse.
Conclusion
Our tests suggest the median CPI is useful tool for forecasting inflation. As such, it should prove useful in helping to gauge room between the near-term trend and the new inflation threshold.
The use of the median CPI also has other benefits. First, it’s the easiest trimmed mean to conceptualize, as it’s simply the price change in the middle of the distribution. But it also holds an important communications advantage over the oft-used core CPI.
In times when the relative prices of energy and food items are rising rapidly, use of the exclusionary core CPI makes the FOMC appear to be disconnected or insensitive, as it disregards subsistence items that consumers purchase much more frequently than, say, cars or new televisions. In communicating the stance of underlying inflation, hitting the one in the middle is far superior to excluding consumer necessities like food and energy.
Footnote
- We focus on inflation statistics based on the Consumer Price Index (CPI) in this Commentary because it is the most recognizable measure of retail prices. However, using the FOMC’s preferred inflation measure the Personal Consumer Expenditures (PCE) Chain Price Index would yield qualitatively similar results. Detmeister (2011) is a good investigation of underlying inflation measures using PCE prices. Return to 1
- Meyer and Venkatu (2012) use the Diebold-Mariano equality of prediction test on the difference in squared forecasting errors between the candidate trim and the lowest mean squared error trim over that sample period. To account for serial correlation, they use the quadratic-spectral kernel and Andrews (1991) bandwidth. The blue swath represents nonrejection of the null hypothesis of no difference in accuracy at a 10 percent significance level. Return to 2
- For a quick primer on the differences between the two indexes see www.bls.gov/opub/btn/archive/differences-between-the-consumer-price-index-and-the-personal-consumption-expenditures-price-index-pdf.pdf. Return to 3
Recommended Reading
- “Trimmed-Mean Inflation Statistics: Just Hit the One in the Middle,” Brent Meyer and Guhan Venkatu, 2012. Federal Reserve Bank of Cleveland, working paper no. 12-17.
- “Bayesian VARs: Specification Choices and Forecast Accuracy,” Andrea Carriero, Todd Clark, and Massimiliano Marcellino, 2011. Federal Reserve Bank of Cleveland, working paper no. 11-12.
- "It’s Not Just for Inflation: The Usefulness of the Median CPI in BVAR Forecasting,” Brent Meyer and Saeed Zaman, 2013. Federal Reserve Bank of Cleveland, working paper no. 13-03.
- “The Usefulness of Core PCE Inflation Measures,” Alan K. Detmeister, 2011. Federal Reserve Board, Finance and Economics Discussion Series 2011-56.
Suggested Citation
Meyer, Brent, Guhan Venkatu, and Saeed Zaman. 2013. “Forecasting Inflation? Target the Middle.” Federal Reserve Bank of Cleveland, Economic Commentary 2013-05. https://doi.org/10.26509/frbc-ec-201305
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International





