- Share
Demographic Differences in Inflation Expectations: What Do They Really Mean?
It has often been reported that different demographic groups show persistent differences in their inflation expectations. Some reasonable explanations have been suggested, but most have failed to fully explain these apparent differences. We argue that the demographic differences have been overstated by using the mean to describe differences across demographic groups. When we use the median to describe inflation expectations, we find little meaningful difference across demographic groups.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
It has often been reported that different demographic groups show persistent differences in their inflation expectations. Some reasonable explanations have been suggested, but most have failed to fully explain these apparent differences. We argue that the demographic differences have been overstated by using the mean to describe differences across demographic groups. When we use the median to describe inflation expectations, we find little meaningful difference across demographic groups.
Most macroeconomists have come to believe that inflation expectations are a key determinant of actual inflation. This clearly has important implications for policymakers. As Federal Reserve System Chairman Ben Bernanke observed in 2004, “. . . an essential prerequisite to controlling inflation is controlling inflation expectations.” Consequently, monitoring and measuring the public’s inflation expectations is of enormous importance to the monetary authority.
There are several ways to measure these expectations. They can be inferred from financial instruments or modeled more explicitly. But the most straightforward way to assess the public’s expectations on inflation is to simply ask American households.
Unfortunately, survey measures of the public’s inflation expectations tend to generate responses that appear at odds with actual experience. And systematic differences across demographic groups that aren’t easily explained by economic factors have led some to wonder whether these surveys are actually providing meaningful information on inflation expectations to policymakers.
However, we argue that these demographic differences have been overstated by previous research, and that by measuring average inflation expectations in a particular way, we can see that these survey measures are indeed informative, whether for a given demographic group or across an entire survey.
Different Groups, Different Inflation Expectations?
The University of Michigan conducts one of the longest-running surveys of American households. Each month, a minimum of 500 interviews are conducted by phone, with samples designed to be representative of all American households, excluding those in Alaska and Hawaii. These monthly surveys contain approximately 50 core questions, each of which tracks a different aspect of consumer attitudes and expectations. Regarding expectations of inflation, the following question has been asked of survey participants since the early 1980s:
“During the next 12 months, do you think that prices in general will go up, or go down, or stay where they are now?”
One of the odd aspects of the responses to this question is that different demographic groups seem to show persistent differences in their inflation expectations, even after adjusting for economically relevant factors.
It isn’t necessarily surprising that households have a range of inflation expectations. After all, households can have different inflation experiences, depending on the things they buy (their “market basket”). In fact, one recent study showed that these differences can be considerable—as much as 1 to 3 percentage points per year. However, the average differences in inflation experiences across groups—less than half a percentage point at most annually—turn out to be notably smaller than the differences in groups’ inflation expectations. Market-basket differences, then, don’t seem adequate to explain the differences in inflation expectations that we observe across groups.
An illustration of these differences can be seen with gender. If we adjust for race and education by restricting our comparison to white, college-educated individuals, women’s inflation expectations remain consistently higher than men’s throughout the last decade (figure 1).
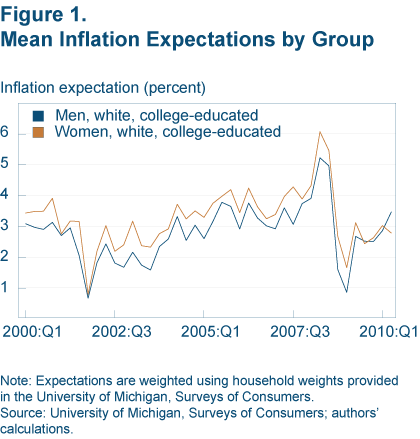
Previous studies show similar patterns. A study by Mike Bryan and Guhan Venkatu shows a persistent gap for an earlier period, after trying to control for differences in income and marital status; and a study using inflation perceptions data from Swedish households in 1977 documents a difference between men and women, also after adjusting the groups to make them more similar. The Swedish study’s author concludes that the observed difference might reflect the fact that women tend to make most of the food purchases in a household. Since Swedish food prices were rising more rapidly than most prices at the time, this seemed plausible. However, subsequent surveys in the United States show the same pattern for men and women, over periods when food prices are actually rising less rapidly than most other prices. Moreover, men’s and women’s perceptions of price changes for the same items show differences too, suggesting that the explanation for the persistent gap in inflation expectations we observe might run deeper than mere market-basket differences.
Measuring the Average
So, what’s driving these differences? There are a number of possible explanations, but the one we find most convincing is that we’re simply mismeasuring average expectations. When we compare various groups’ inflation expectations and conclude that they are different, we’re generally comparing their means. But a better measure of the average is probably the median because of the way these survey responses tend to be distributed.
Figure 2 shows the median inflation expectation for the same two groups as shown in figure 1. To find this measure of the average, we arrange survey participants’ responses from lowest to highest and find the response in the middle of the array; that response is the median. By construction, half of our responses are above the median, while half are below it.
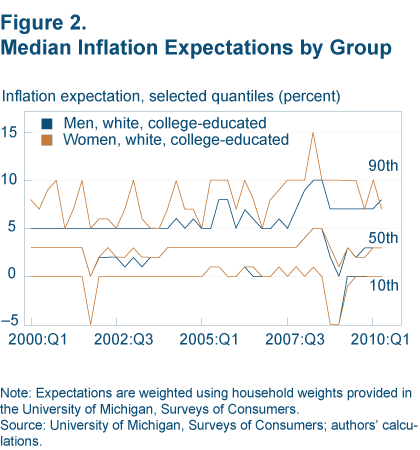
One advantage of using the median rather than the mean is that it isn’t sensitive to the extreme responses that may skew a distribution. An example often used to illustrate this point relates to income. Just a few very high-income individuals can dramatically affect the mean. For instance, imagine an economy with 10 people, where 9 have incomes of $100 and 1 has an income of $10,000. The median income in this hypothetical economy is $100, while the mean income is $1,090. If we want to use the average to summarize living standards for a typical person in this economy, the mean might lead us to believe that this person is more than 10 times richer than is the case. The median, on the other hand, successfully describes incomes for most individuals in this economy. Accordingly, we typically think of median income as a more informative statistic than mean income.
The same logic might also apply to inflation expectations. Indeed, if we were to use the median to measure average expectations, we would come to a different conclusion than if we were to use the mean. The former suggests that there is in fact very little difference in inflation expectations between white, college-educated men and women. The latter, however, as in the income example, is influenced by a small number of relatively high responses and, as a result, appears to show a difference between the two groups.
We can see this clearly by looking at a couple of points on the distribution of inflation expectations responses. The first such point is at the 90th percentile. If, when considering only college-educated white women, we were to select the response that was greater than 90 percent of the other responses for this group, we would find that this value is frequently several percentage points higher than the comparable figure for college-educated white men. Put simply, the highest responses for women are higher than the highest responses for men.
However, the distribution of responses looks very similar for the two groups up to the 60th percentile. It’s only after this point that women begin to consistently report higher expectations than their male survey counterparts. The question—thinking back to the income example—is: Do we want to use the differences among the two groups’ more extreme observations to help us characterize their average tendencies?
An example from the medical field might further clarify things. If a drug trial showed that, on average, women derived benefit from some treatment while men derived no benefit and suffered side effects as well, a doctor might decide quite reasonably to prescribe this treatment only for his female patients. But what if the average benefit shown for female study participants was actually associated with only a few women who saw dramatic improvements, while most women had the same outcomes as men? In this instance, it seems it would be irresponsible to prescribe the treatment to women as a matter of course. Some women may see significant benefits from the treatment, but most would not and many may suffer side-effects as well. This suggests the problem with relying on the mean without a more complete understanding of the full distribution of outcomes.
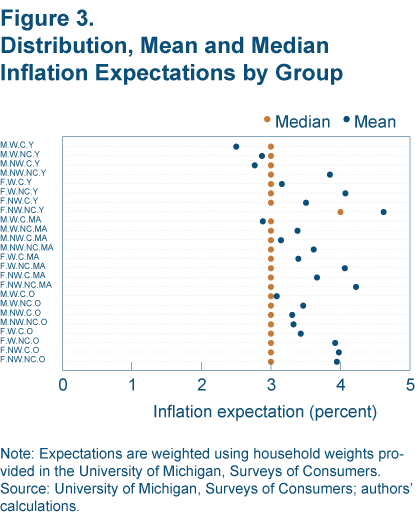
Performing the same exercise as we did for gender for different demographic groups shows the same basic result: different means, but no difference in the medians. Figure 3 shows means and medians from January 2000 to June 2010 for 24 nonoverlapping groups. The groups are formed from two categories for gender (male and female), race (white and non-white), and education (college and non-college), and three categories for age (young: 18-39; middle age: 40-59; and old: over 60). For instance, M.W.C.Y is male, white, college-educated, and young.
It’s fairly obvious from figure 3 that, aside from one category, there are no differences in the medians across these categories. However, these data were combined across surveys spanning 10 years. Combining the data in this manner implicitly assumes that there are no important differences in the distribution of responses across surveys—that a relatively tranquil month in 2005 is the same as December 2008, when we were in the throes of a financial crisis. That is not the case. For instance, in the summer of 2008, prior to the onset of the most acute phase of the financial crisis, median inflation expectations stood at about 5 percent. But by the end of the year, this figure had fallen to about 2 percent.
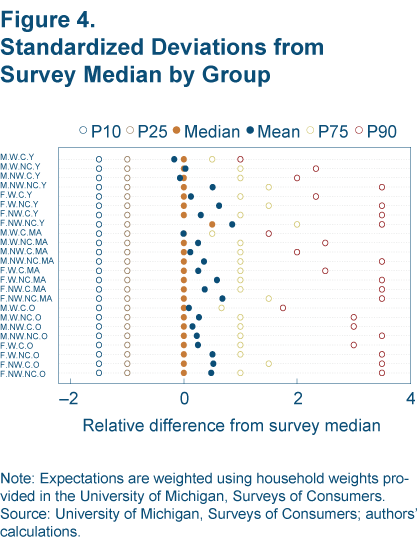
In order to have confidence in our results, we transform the data to remove survey-specific differences in the levels and variability of inflation expectations. These transformations give us re-scaled responses and leave only the relative differences between respondents, which is what we’re interested in understanding. After we’ve removed these survey-specific factors, we can combine responses across multiple surveys.
The way we do this is to express every response relative to its survey average. This reconstructed value will indicate how many percentage points a response is above or below the typical (or average) response in the same month. In this case, for the reasons mentioned earlier, we’ll use the median as our measure of the typical or average response.
Similarly, because of changing economic conditions, the range of responses can vary from month to month. That is, some surveys might exhibit relatively more agreement among respondents than others. As 2008 wore on, for instance, survey respondents started to show greater disagreement (as measured by monthly survey variance) in their inflation expectations.
We adjust for this also, and express our reconstructed responses as a proportion of the average amount of disagreement (or variability) in a given month. In this case, we measure variability as the average absolute distance of all responses in a month from that month’s median response. Again, when we take the average absolute distance, we measure average as the median rather than the mean.
While we might have more confidence in combining these transformed data from more than 100 individual surveys, the new data (in figure 4) don’t meaningfully alter the basic pattern shown previously by the untransformed data in figure 3. Despite differences in the means, outside of one category, there aren’t any differences in the medians. We can also clearly see what we observed when looking at the time-series plot for college-educated, white men and women. There is tremendous similarity across groups in the lower half of the distribution, but somewhere between the 50th and the 75th percentiles, differences begin to emerge. These differences become even more pronounced at the 90th percentile.

Should we use groups’ more extreme observations to help us characterize their average tendencies? We think the answer is no. Relying on means emphasizes the differences that exist across groups primarily among their most extreme high responses and obscures the overlap that exists across much of the rest of their distributions.
To put it differently, it isn’t that men and women, in general, are providing very different forecasts of inflation; it’s that some women—a relatively small subset—are. But it would be a mistake to ascribe these more extreme views to that group as a whole. Using the median avoids this problem. And when we use the median, it suggests, in general, that there aren’t meaningful differences in inflation expectations across different demographic groups.
A Possible Cause of the Variation
Still, a question remains about what is causing the differences in inflation expectations across groups toward the high end of their distributions. One possible explanation uncovered by other researchers relates to financial literacy.
Wändi Bruine de Bruin and fellow researchers from Carnegie Mellon University and the Federal Reserve Bank of New York noted that several previous studies had shown lower financial literacy in the demographic groups that tend to overestimate inflation: women, singles, some minorities, and those without a college education. (Mary Burke, at the Federal Reserve Bank of Boston, noted a similar association.) In addition, they found that these groups were more likely to provide responses above a certain high threshold (in this case, 5 percent). They also found that adding financial literacy as an explanatory variable reduced the importance of several demographic factors, specifically, gender, education, and income.
This evidence appears to be consistent with what we observe in the data from the University of Michigan: stability in inflation expectations across groups, until we get toward the higher-value responses. While we have previously ascribed the demographic differences we see when examining means to the groups themselves, it appears that another attribute—low financial literacy—may actually have been driving the differences instead. Since these low financial literacy respondents are often providing answers that are well above average, and because they are disproportionately associated with different demographic groups, it makes sense that the differences we observe in inflation expectations across groups appear in the upper half of these distributions. The effect is to skew the mean, in a way that may not effectively describe expectations for a typical respondent in a given demographic group. As in the income example, using a median addresses this potential problem.
Finally, we know that using the median of the entire survey is a fairly accurate predictor of future inflation—typically more accurate than the forecasts from simple models and about as accurate as the forecasts from professional forecasters. However, a concern about using a median (or trimmed-mean) was that it would disproportionately screen out some demographic groups (which had higher representation in the tails). But perhaps all that’s happening is that the influence of less financially literate individuals is being reduced, thereby improving forecast accuracy relative to the mean.
Aside from forecast accuracy, however, the argument for using the median is that it may simply be a better way to describe the average in these data. When we take medians within narrowly defined demographic groups, we see essentially no differences in their inflation expectations, and this—as in the case of the overall survey—may be a much more informative measure of inflation expectations for these groups than their corresponding means.
Recommended Reading
- “The Curiously Different Inflation Perspectives of Men and Women,” Michael F. Bryan and Guhan Venkatu. 2001. Federal Reserve Bank of Cleveland, Economic Commentary(November).
- “The Demographics of Inflation Opinion Surveys,” by Michael F. Bryan and Guhan Venkatu. 2001. Federal Reserve Bank of Cleveland, Economic Commentary (October).
- “Economic Literacy and Inflation Expectations: Evidence from an Economic Experiment,” by Mary Burke and Michael Manz. 2010. Unpublished manuscript.
- “The Evolving Inflation Process: An Overview,” by Gabriele Galati and William Melick. 2006. BIS working paper no. 196.
- “Expectations of Inflation: The Role of Demographic Variables, Expectation Formation, and Financial Literacy,” by Wändi Bruine de Bruin, Wilbert van der Klaauw, Julie S. Downs, Baruch Fischhoff, Giorgio Topa, and Oliver Armantier. 2010. Journal of Consumer Affairs, 44(2): 381–402.
- “Perceived and Expected Rates of Inflation in Sweden,” by Lars Jonung. 1981. American Economic Review, 71(5): 961-68.
- “Simple Ways to Forecast Inflation: What Works Best?” by Mehmet Pasaogullari and Brent Meyer. 2010. Federal Reserve Bank of Cleveland, Economic Commentary (December).
- “The Term Structure of Real Rates and Expected Inflation,” by Andrew Ang, Geert Bekart, and Min Wei. 2007. NBER working paper, no. 12930.
Suggested Citation
Meyer, Brent, and Guhan Venkatu. 2011. “Demographic Differences in Inflation Expectations: What Do They Really Mean?” Federal Reserve Bank of Cleveland, Economic Commentary 2011-07. https://doi.org/10.26509/frbc-ec-201107
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International




