An Assessment of the ISM Manufacturing Price Index for Inflation Forecasting

One of the timeliest inflation indicators available is the price index released as part of the monthly Manufacturing ISM Report on Business, which we will refer to as the ISMPI.¹ For instance, the release of ISMPI data precedes the release of the consumer price index and the personal consumption expenditures price index by roughly 2 and 4 weeks, respectively. The ISMPI is a measure of pricing trends constructed from a survey of a nationwide sample of purchasing and supply executives, in which respondents are asked whether they see the prices of their inputs as increasing, decreasing, or staying the same over the month.²

There are reasons to think that the ISMPI could have predictive content for producer and consumer price inflation. To the extent that there are cyclical movements in inflation, some sectors, such as manufacturing, might show them before the broader consumer and producer price indexes. Furthermore, to the extent that the surveyed manufacturers are largely producing inputs to other goods, one might expect the increasing price pressures they face to show up in the markups they charge to producers at the next link in the production chain and so on before goods are finally sold to consumers. For example, in the most basic version of benchmark macroeconomic models, consumer prices are a fixed “mark-up” over the prices charged by intermediate goods producers.³

However, attractive though the theoretical link between manufacturing prices and broader inflation measures might be, it could instead be the case that the particular construction of the ISMPI differs so much from that of broader inflation measures that the ISMPI ultimately provides more “noise” than “signal” for broader inflation measures.⁴ Ultimately, the question of whether or not the ISMPI contains useful information for forecasting broader inflation aggregates is an empirical one, and one which has seen little examination to date.⁵ In this article we take a step toward examining the ISMPI’s information content by assessing its ability to improve inflation forecasts of up to 12 months ahead for producer and consumer prices as measured by three broad monthly inflation measures:⁶

• Producer price index (PPI) for intermediate processed goods
• Personal consumption expenditures price index (PCEPI)
• Core PCE price index, the PCEPI excluding food and energy (core PCEPI)

We focus on these three inflation aggregates for the following reasons. The ISM emphasizes the predictive capacity of the ISMPI for the PPI for intermediate goods, and, at a minimum, one would hope to find predictive capacity here. The PCEPI is the Fed’s preferred inflation measure for assessing achievement on its stated inflation target and the core PCEPI is a widely used proxy for the trend in the PCEPI. The possibility that predictive content could pass through to these more widely tracked inflation measures follows from the input–output-markup mechanism described above.

As a preview of the results, we will find that the ISMPI has some predictive content for producer prices; however, this property appears not to pass through to predictive content for consumer prices.

Quantitative Relationships to Broader Inflation Measures

In addition to the conceptual arguments mentioned above, a first-pass at the quantitative evidence suggests that the ISMPI could have predictive capacity for broader inflation measures. Figure 1 plots the time series of the ISMPI along with each of the inflation measures, each of which has been standardized to best match the scaling of the ISMPI.⁷

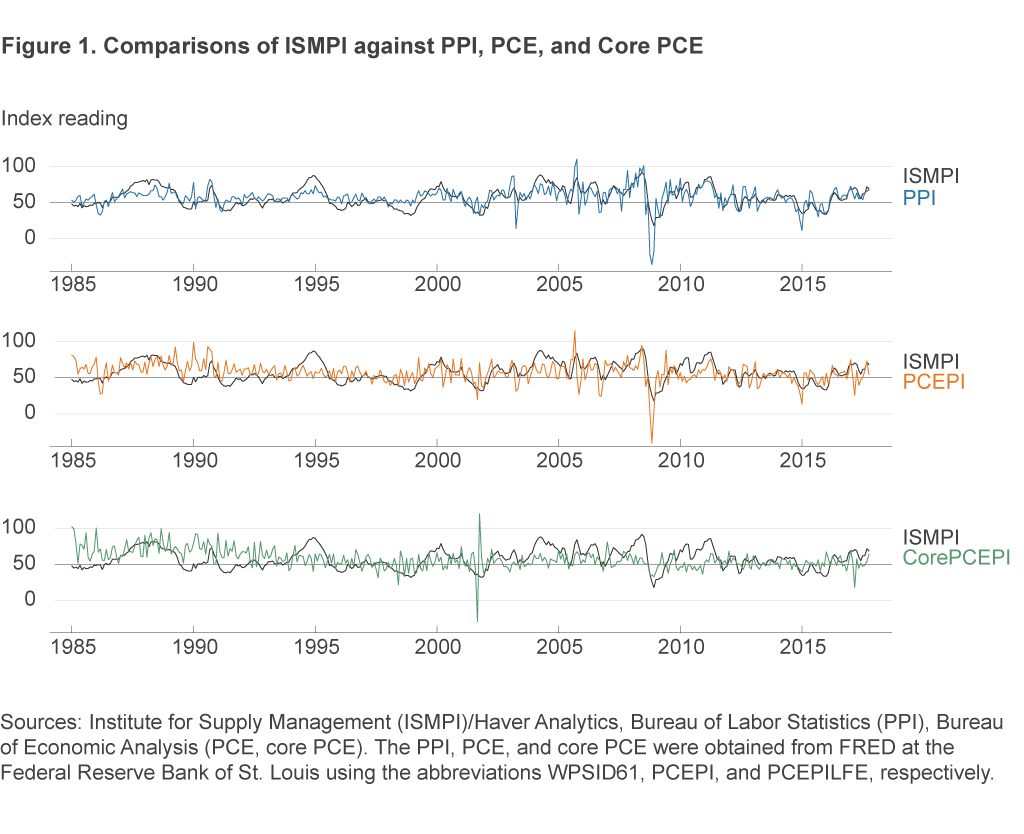
While the relationships contain plenty of noise from one month to the next, some degree of a positive historical relationship between the ISMPI and each of the inflation measures is visually apparent, particularly from 2000 onwards. Using the eyeball test, one might reasonably say that the relationship to the ISMPI appears closest for the PPI, less close for the PCEPI, and almost pure noise for the core PCEPI, and, indeed, quantifying the relationships by computing correlations yields that conclusion.

Figure 2 plots the correlation between the ISMPI and each of the inflation measures, with the ISMPI taken at leads and lags of up to 12 months.⁸ Each line traces out the values of the computed correlations at the different leads and lags for a given inflation indicator. The values along the horizontal axis indicate the relative timing of the ISMPI to the inflation indicators, with negative numbers indicating a lead of the ISMPI value relative to the inflation indicator. The value of 0 along the horizontal axis of the figure shows the contemporaneous correlation between the ISMPI and each inflation measure, while at a value of –3 the figure shows the correlation of the ISMPI’s value at 3 months prior to the inflation indicators. Substantial positive values for a given line in the left half of the figure would then indicate a systematic positive relationship between the ISMPI and later values of the inflation indicator and thus the potential for predictive capacity in the ISMPI for that indicator.

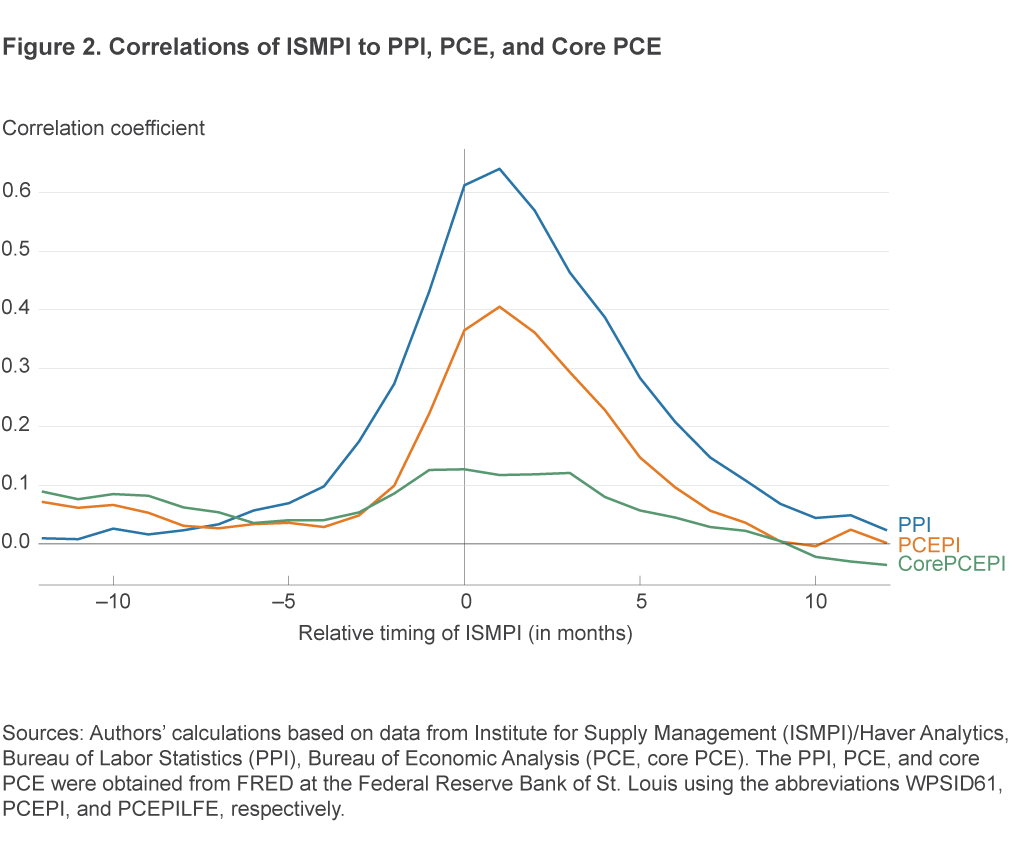
As it happens, the ISMPI indeed does have a substantive positive leading correlation with broader inflation measures, most significantly the PPI but also the PCEPI. The ISMPI two months ahead has correlations of 0.27, 0.10, and 0.09 with the PPI, PCEPI, and core PCEPI, respectively, and, at one month ahead, correlations of 0.43, 0.22, and 0.13. These correlations are not overwhelmingly strong, but nor are they negligible, and they suggest the potential for the ISMPI to contain useful information about near-term inflation.

Assessing the Predictive Content

Building on the results in the previous section, we assess the predictive content of the ISMPI in the context of forecasting models. Research has shown that the persistence of inflation means that past inflation has substantial predictive value for future inflation. For evaluating other predictors, such as the ISMPI, it is common to set up models that embed this idea and then to add the other indicators to see if they improve predictions.

To be more specific, we consider forecasting regressions for average inflation rates of each price index over horizons from 1 to 12 months ahead, with the annualized average inflation rate over the next h periods denoted as π_t,t+h.⁹ The regressions include the value π_t−12,t among the predictors, or the inflation rate during the last year, and the value of the ISMPI at time t, ISMPI_t. Thus the regressions take the form

(1) π_t,t+h = b₀ + b_π × π_{t − 12,t+} + b_ISM  × ISMPI_t + e_t.

The coefficients b₀ , b_π, and b_ISM  are values to be estimated from the data. The coefficient b₀  is a constant term that reflects the long-run mean of the inflation rate being forecasted, the coefficient b_π gives the effect of a 1 percentage point increase in the average inflation rate over the last year, and the coefficient b_ISM gives the effect of a one-unit increase in the ISMPI_t on the inflation forecast. At each point in time, the forecasts are constructed from the relationship in equation (1) by first estimating all of the b coefficients from historical data and then plugging in the observed values of the data for the inflation rate, π_t−12,t, and the ISMPI, ISMPI_t .

Data, Estimation, and Forecast Evaluation

In model-based forecasting exercises, choices must be made about which observations to use for the estimation of the econometric models’ parameters and about which observations to use for evaluating the accuracy of each model’s forecasts. We chose the samples by following standard choices in the literature: The estimation of our forecasting models uses data beginning in January 1960, and the forecasting evaluation begins with forecasts from January 1985 and running to October 2017.¹⁰

The forecasting exercise is recursive and pseudo-real time. This means that beginning with January 1985, we estimate the parameters of each model and produce forecasts for each forecasting horizon. Moving to the next month, February 1985, we then re-estimate the parameters of all models in light of the additional data point that has become available and produce forecasts, and so on, proceeding one month at a time until the end of the sample.¹¹ With more than 30 years of monthly data in the forecast evaluation sample and 12 different forecasting horizons for each of three distinct inflation indicators, this exercise entails roughly 13,000 separate model estimations.

Having tabulated the forecasts, we assess each model’s forecast accuracy on the basis of root mean squared prediction error (RMSPE). The RMSPE is a standard forecast evaluation metric that penalizes forecasts for how far away they are from the realized value of the forecasted variable. Hence, better forecasting models have smaller RMSPEs, with zero as the best possible value of RMSPE. RMSPE is calculated as

(2)

wherein the term  is the realized value of the annualized average inflation rate for indicator j over the period from t to t+h, and  is the forecasted value of that inflation rate.

Forecasting Results

Figure 3 shows the forecasting results. Each panel shows, for a single inflation indicator, the results for all forecasting horizons from both the model with, and the model without, the ISMPI.

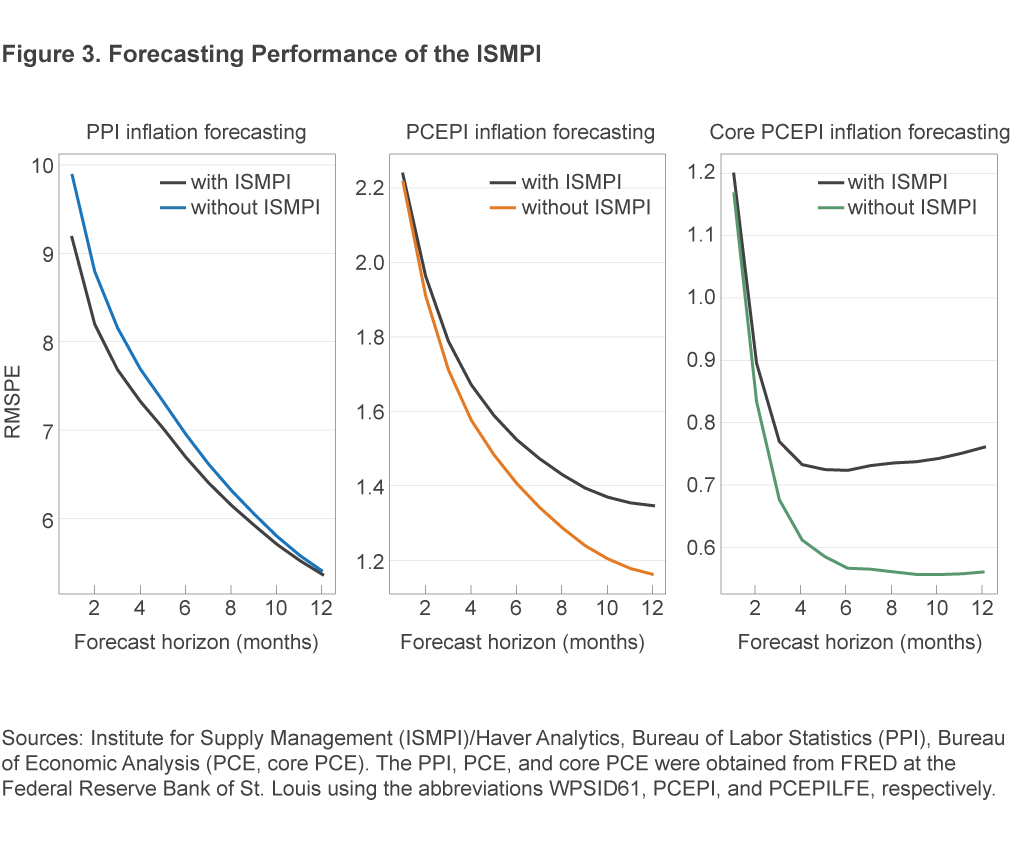
The vertical axis in each panel shows the RMSPE from the forecasting model for annualized average inflation at horizon h indicated by the value on the horizontal axis. The values connected by a line in a given plot are the RMSPEs of the models that include the same set of predictors, namely, the ISMPI or not. Hence, whenever the line representing the models that include the ISMPI lies below the line for models without, this means that the ISMPI improves forecast accuracy relative to the benchmark model.

From the plots, we can see that the ISMPI improves forecast accuracy for the PPI and does so primarily at forecasting horizons of less than 6 months. Specifically, the RMSPE for forecasting PPI inflation falls by 0.72 (roughly a 7 percent smaller RMSPE) relative to the benchmark model when forecasting inflation one month ahead. The 0.72 unit improvement can be seen graphically in figure 3 as the vertical distance between the two lines in the “PPI inflation forecasting” panel. The gains then decline smoothly through the maximum forecasting horizon of 12 months, at which point the gains are virtually 0. On the other hand, the models with the ISMPI forecast PCE inflation and core PCE inflation more poorly than the models without. Forecasts for PCE inflation and core PCE inflation are virtually identical with and without the ISMPI at the one- and two-month horizons, but the extent to which the ISMPI models forecast more poorly than their benchmarks in terms of RMSPE units steadily increases to 0.19 (a 16 percent greater RMPSE) and 0.20 (a 36 percent greater RMSPE) at the 12-month forecasting horizon for PCE inflation and core PCE inflation, respectively.

Note that in any exercise such as this one, there is a question of how confident one can be that the results are not, in some sense, the result of randomness. Even if two models have, on average, equal predictive capacity, in any finite sample of data one model will likely outperform the other. In the context of the results from other forecasting exercises on macroeconomic data, the gains for the short-term PPI inflation forecasts would be near the boundary of gains that would be considered statistically significant, while the differences for PCE inflation and core PCE inflation are likely insignificant.

One might wonder how the inclusion of an extra predictor could worsen the average forecast. This is where the recursive estimation out-of-sample forecasting procedure is key. If the extra indicator lacks a stable relationship with the forecasted variable, then the repeated estimations will yield fluctuations in the estimated value of bISM when new data become available. The fluctuations in bISM will create instability in the forecasts from one period to the next and deteriorate average accuracy. In this fashion, the RMSPE penalizes the inclusion of additional predictors whose relationship to the forecasted variable turns out to be unreliable.

Robustness

We assess the robustness of the results in the previous section to two alternative forecasting specifications in which, rather than using the most recent value of the ISMPI as a predictor, the average value of the ISMPI over the previous 3 months or 6 months is used as a predictor. Figure 4 shows the RMSPEs from these additional models, along with the benchmark model that excludes the ISMPI.

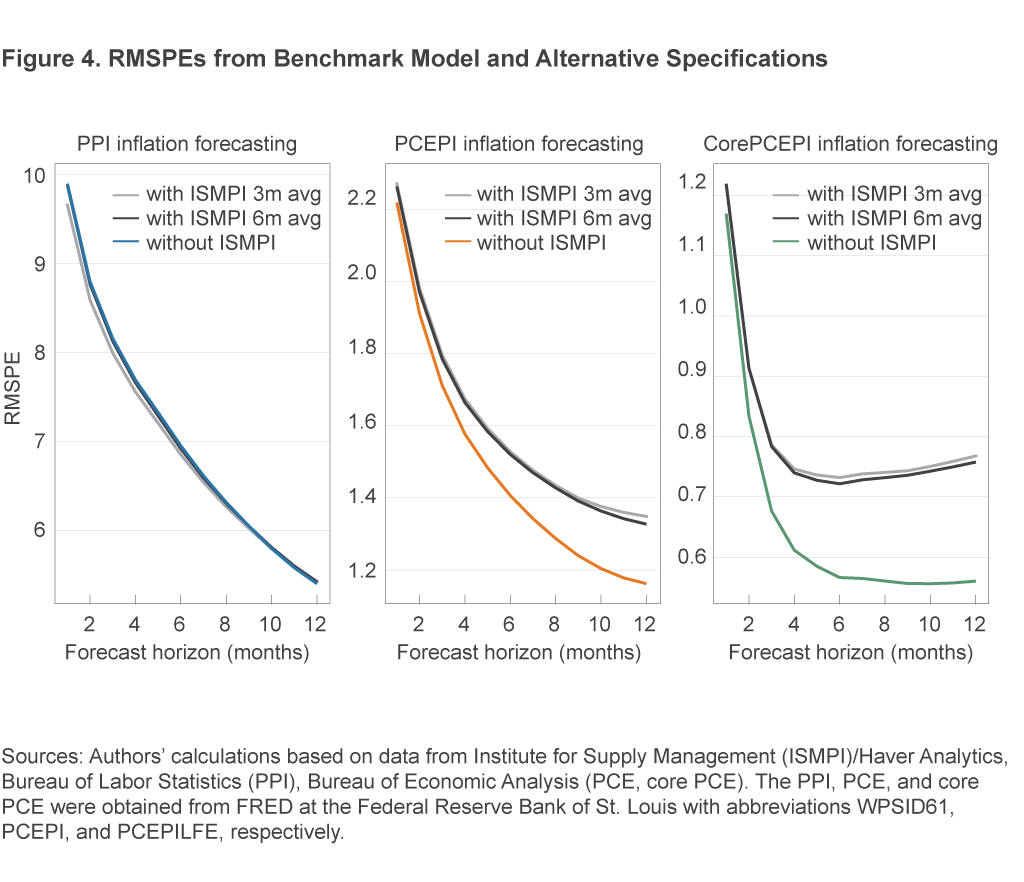
One can see that the results from the two additional models are almost identical to each other; indeed, the lines are difficult to distinguish. The results are also similar to those from the model in the previous section: The inclusion of the ISMPI yields small forecasting gains for the PPI at shorter horizons, though not for PCE inflation and core PCE inflation. The results from the robustness exercise allow us to be more confident that our main results from the previous section are not a fluke resulting from our particular choice of how to use information from the ISMPI in the forecasting regressions.

Conclusion

In this article, we examined the relationship between the ISMPI and broader inflation aggregates. We documented positive correlations between the ISMPI and inflation in the PPI, PCE price index, and core PCE price index. To further explore how these relationships might be used by policymakers, we examined the performance of forecasting regressions with and without the ISMPI among their set of predictors. Looking at the predictive content for annualized average inflation rates over forecasting horizons from 1 to 12 months, we found that the ISMPI improved forecasts of PPI inflation, particularly at shorter horizons. The ISMPI did not yield improved forecasts of PCE inflation or of core PCE inflation.