- Share
Adding Double Inertia to Taylor Rules to Improve Accuracy
A Taylor rule captures the historical behavior of the federal funds rate better when it also includes a partial-adjustment factor. Typically, the type of partial adjustment added is consistent with the FOMC avoiding large jumps in the level of the funds rate. We add another type of partial adjustment—consistent with the FOMC avoiding changes in the pace of change and improve the rule’s historical fit.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
The Taylor rule is an equation which is used to describe the factors that have helped shape past monetary policy decisions. The rule expresses the federal funds rate—the short-term interest rate at which banks lend to each other—in terms of the rate of inflation and the gap between the economy’s current performance and its full potential, and it has been argued that it captures the historical behavior of the funds rate fairly well.
But previous work suggests that the rule does a better job when it includes some partial adjustment of the funds rate toward this rule, in which case the funds rate given by the rule is more of an intermediate funds rate target. Said another way, the partial-adjustment factor reflects the likelihood that the Federal Open Market Committee (FOMC) moves more slowly than the Taylor rule predicts. This inertia suggests that the FOMC dislikes large changes in the level of the funds rate.
We argue that another type of inertia is important for understanding how the funds rate was set in the past. In addition to disliking large changes in the level of the funds rate, the FOMC might also have wanted to avoid any change in the pace of change it had been making to the rate. For example, if the FOMC had been steadily reducing rates by 25 basis points over the past few meetings, it might be a little reluctant to then decide to keep rates constant or to reduce rates by 50 basis points.
This type of inertia could arise if the FOMC is focused more on changes in the funds rate and not the level of the funds rate. In this Commentary, we compare these two versions of inertia and show that a rule reflecting adjustments for both changes of the funds rate as well as the level of the funds rate helps explain past policy decisions better.
There are at least two motivations for capturing historical US monetary policy with an equation like the Taylor rule. First, policymakers may want to use the estimated policy rule as a guidepost in setting current policy. After all, if policy has been successful in the past, then one might want to continue with it. Policymakers will want to deviate from such a guidepost based on information not contained in the rule, but the rule remains useful as a guidepost. Second, the public may use the estimates of historical policy provided by the rule to get a better idea of the future course of monetary policy over both the short and long term.
Second, the public may use the estimates of historical policy provided by the rule to get a better idea of the future course of monetary policy over both the short and long term. Although the federal funds rate has been near zero since the financial crisis and the FOMC has indicated that it will likely be there for a considerable time, eventually short-term interest rates will increase and become important again in monetary policymaking. When that happens, there will be renewed interest in predicting where these rates will be in the future.
The Intermediate Rate Target
The usual partial adjustment or inertial Taylor rule has the FOMC slowly adjusting the funds rate (level) toward an intermediate funds rate target. We assume that the funds rate given by the simple noninertial Taylor rule is the FOMC’s intermediate target. The basic version of the Taylor rule we use in this Commentary expresses the funds rate as a function of movements in inflation and the unemployment rate (as the unemployment rate is one way to capture the gap between current and full economic potential). This is a natural choice, as the Federal Reserve’s statutory mandate includes both price stability and maximum employment.
Estimating a simple rule of this type from 1987 to 2008 (when the fed funds rate fell to nearly zero percent) yields the following equation
TRt = FFRLR + 1.73(inft − infLR) − 1.77(URt − URLR),
where
TRt is the current funds rate given by the Taylor rule,
FFRLR is the Fed’s long-run funds rate goal,
inft − infLR is the gap between the current PCE inflation rate and the Fed’s long-run PCE inflation rate goal (currently 2 percent), and
URt − URLR is the gap between the current unemployment rate and the long-run unemployment rate.
According to this rule, inflation above its long-run target will lead to an increase in the funds rate, and unemployment above its long-run trend will lead to a decrease in the funds rate.
The two versions of the Taylor rule we compare are different interpretations of a partial-adjustment rule. The first version assumes that policy changes are determined by how far the funds rate is from the intermediate target. Below we show that this expression for policy is equivalent to a policy in which the FOMC adjusts the level of the funds rate only partially to its intermediate target (because of this equivalence, we call it the partial-adjustment level rule). The second description of historical policy we consider is one in which the change in the funds rate reacts both to the gap between the funds rate and its intermediate target and the most recent change in policy. We call this version the partial-adjustment change rule.
To understand why a change rule may be preferable, consider a metaphor. Suppose a boat is heading into harbor, and the skipper is choosing the speed he needs to go currently to arrive at his chosen pier (target). Under a level policy, this speed is independent of the past speed and depends only on his current distance from the pier. But such a policy may imply a very sharp acceleration or deceleration, which could be uncomfortable for the passengers (markets). Under a change policy, the skipper considers both the distance from the pier, and his recent speed. This will imply a smoother path into the harbor.
Two Ways to Model Gradual Policy Changes
The level description of policy assumes that the FOMC moves the level partially toward its intermediate target. We therefore estimate the predicted funds rate as a partial adjustment in the level of the funds rate given by the Taylor rule equation above (TRt):
Rt=(1 − 0.095)Rt−1 + 0.095TRt.
That is, the predicted funds rate is the intermediate target given by the Taylor rule, adjusted by a portion of the last period’s funds rate (specifically, 1 − 0.095). In other words, this estimate suggests that after each meeting, the FOMC has historically moved 9.5 percent of its way toward its intermediate target. This level of adjustment (or inertia, as theorists call it) suggests that after eight quarters the funds rate would be a little over halfway toward its intermediate target.
Another way of expressing this relationship is by rewriting the partial-adjustment policy into a policy in funds rate changes:
ΔRt = 0.095(TRt − Rt−1),
where ΔRt = (Rt − Rt−1) is the change in the funds rate. Again, the positive coefficient in this relationship is not surprising. If the recent funds rate is below the target
(TRt > Rt−1), then the change in the funds rate has been typically positive, and vice versa.
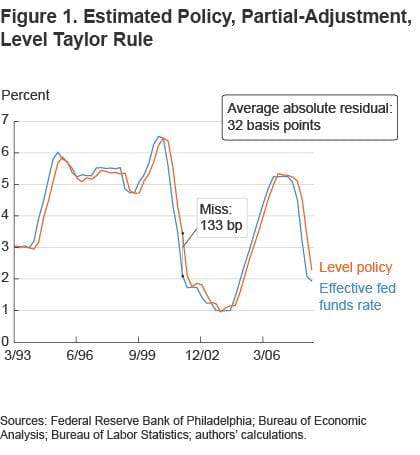
Figure 1 plots the level of the funds rate predicted by the partial-adjustment level Taylor rule against the actual funds rate. At first glance, this rule tracks the funds rate remarkably well. But looks can be deceiving. The deviation of the funds rate from its predicted value is given by the vertical distance in the figure. Take the end of 2001, for example. The miss on that date was a whopping 133 basis points.
Sources: Federal Reserve Bank of Philadelphia; Bureau of Economic Analysis; Bureau of Labor Statistic; authors' calculations
Since the average funds rate change is 32 basis points, this 133 basis point miss is huge. In fact, the level rule is only slightly better than a simple guess which says today’s funds rate is yesterday’s funds rate. The level policy is a phase shift compared to the actual funds rate, essentially trailing by one quarter.
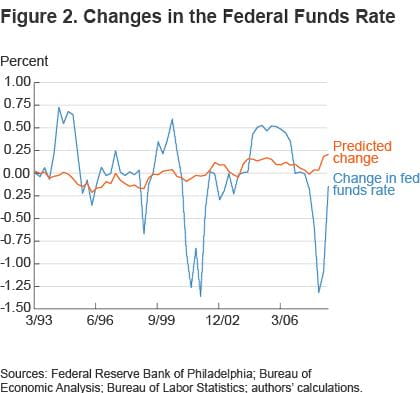
The fundamental problem with the level description of policy is that it assumes that current funds rate changes are independent of past changes. This assumption is wildly counterfactual. Figure 2 plots the actual changes in the funds rate compared to the rate changes estimated under the level policy. It is clear that past policy changes are correlated with current policy changes: if the funds rate decreased last quarter, for example, it is much more likely to decrease again (rather than increase) this quarter.
Sources: Federal Reserve Bank of Philadelphia; Bureau of Economic Analysis; Bureau of Labor Statistic; authors' calculations
Similarly, if we consider FOMC policy from 1989-2008 and focus on times when the funds rate is increasing, the average number of days with no funds rate change is 37 (essentially the interval between meetings), while once the funds rate has plateaued, the average duration with no funds rate change is 219 days. Similar results arise for times when the funds rate is decreasing. In short, the historical data suggest that the FOMC does not like to change the speed of the boat (versus just the position) too abruptly.
Because funds rate changes are correlated with lagged changes of the funds rate, we next estimate the change description of monetary policy. This estimate is given by
ΔRt = 0.738ΔRt−1 + 0.083(TRt − Rt−1).
That is, today’s monetary policy (speed) is related to yesterday’s monetary policy and how far the funds rate is away from its intermediate target given by the basic Taylor rule. Note that the coefficient on the distance from the intermediate target is quite similar to the estimate for the level rule (0.095 compared to 0.083). But there is a significantly positive coefficient on the lagged change in the funds rate, implying that the FOMC historically appears to not like abrupt changes in speed, but prefers the current policy change to be highly correlated with the recent past.
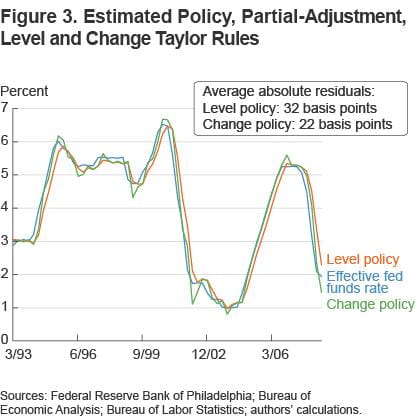
Figure 3 plots the estimated change policy along with the level policy against the actual funds rate. Note first that the improvement in fit is substantial: a reduction of 10 basis points in the residual is sizeable given that the average rate change is 32 basis points. Second, the phase shift is largely absent in the change policy model. There is, however, a small problem with the change policy: it often overshoots the actual funds rate at the end of sustained policy movements. This is not too surprising. The change policy is trying to proxy for the idea that the FOMC does not like to change the course of policy abruptly; that is, other things equal, the FOMC would not want to decrease rates if there is a likelihood that it would need to increase rates in the near future.
Sources: Federal Reserve Bank of Philadelphia; Bureau of Economic Analysis; Bureau of Labor Statistics; authors' calculations
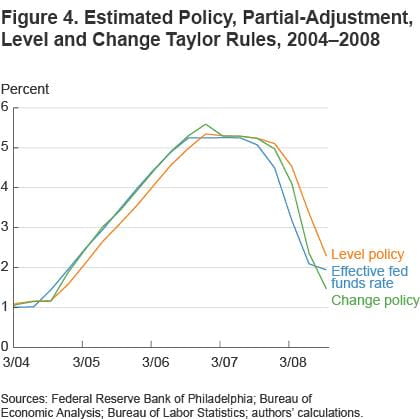
Figure 4 focuses on a subperiod that exemplifies the arguments we have been making. The phase shift under the level policy is quite evident, while there is a substantial improvement under the change policy. For example, during the sustained increase in rates starting in early 2005, the level policy is always a quarter behind, while the change policy is on target. Figure 4 also exhibits the overshooting under the change policy, overshooting at both the end of 2006 and the fall of 2008.
Sources: Federal Reserve Bank of Philadelphia; Bureau of Economic Analysis; Bureau of Labor Statistics; authors' calculations
These episodes might also reflect the fact that the FOMC almost certainly does not mechanically follow a simple policy rule, but responds to other unusual developments in the economy. For example, in the fall of 2008 after the funds rate reached 2 percent, the FOMC moderated the funds rate decline (relative to the change rule). This may have been because of the near proximity of the zero bound and the FOMC’s possible desire to save some policy ammunition for a later date.
Conclusion
In this Commentary we consider two plausible descriptions for historical US monetary policy: a level policy (partial adjustment in levels), and a change policy (partial adjustment in changes). The typical description of FOMC policy is a level policy in which the FOMC moves the level of the funds rate gradually to some target. But we suggest that a better description of past policy is a change policy, in which the FOMC adjusts changes in the funds rate gradually. This is evident in the substantial improvement in the fit of the model (the average miss decreases from 32 basis points to 22 basis points), and in the lack of a phase shift in the change policy.
The Taylor rule is a description of past Fed behavior. The more accurate this description can be made, the more it could potentially help policymakers as a guidepost. Likewise, a more accurate Taylor rule could help the public get a better idea of the future course of monetary policy.
Suggested Citation
Carlstrom, Charles T., and Timothy S. Fuerst. 2014. “Adding Double Inertia to Taylor Rules to Improve Accuracy.” Federal Reserve Bank of Cleveland, Economic Commentary 2014-08. https://doi.org/10.26509/frbc-ec-201408
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International




