Modeling Behavioral Responses to COVID-19
Many models have been developed to forecast the spread of the COVID-19 virus. We present one that is enhanced to allow individuals to alter their behavior in response to the virus. We show how adding this feature to the model both changes the resulting forecast and informs our understanding of the appropriate policy response. We find that when left to their own devices, individuals do curb their social activity in the face of risk, but not as much as a government planner would. The planner fully internalizes the effect of all individuals’ actions on others in society, while individuals do not. Further, our simulations suggest that government intervention may be particularly important in the middle and later stages of a pandemic.
The ongoing COVID-19 pandemic has prompted the development and application of a bewildering array of models designed to forecast the spread of the virus.1 The variety of methods employed in this literature can make it difficult for a reader to assess the importance of individual assumptions in shaping the output of each model. In earlier work2 we discussed a number of epidemiological models and showed how the resulting forecasts for the prevalence of the virus depended upon the network structure between individuals.
In this Commentary, we focus on a different aspect of COVID-19 modeling and show how allowing individuals to alter their behavior in response to the virus both changes the resulting forecast and informs our understanding of the appropriate policy response. In doing so we build upon the canonical SIR (Susceptible-Infected-Removed) model of Kermack and McKendrick (1927) for our modeling of virus transmission. Since that model was published in the 1920s, a vast epidemiological literature has enriched it in innumerable ways, incorporating various forms of heterogeneity in links and risk profiles of individuals.3 However, as noted by Funk, Salathé, and Jansen (2010), such extensions usually do not incorporate behavioral responses. Although economists do not study infectious diseases, we argue in this Commentary that the tools economists routinely employ in modeling decision-making under uncertainty may be incorporated into an epidemiological model to provide new insights.
One benefit of this approach is that it clarifies the role of public policy. Since the onset of the COVID-19 pandemic, governments around the world have sought to control the spread of the virus by restricting social and economic activity. We can explore the optimal form of such lockdowns over time by comparing the outcome when individuals choose their own levels of activity (“equilibrium outcome”) with that arising when the government enforces activity levels that maximize average welfare over time (“optimal outcome”). We show that the levels of activity across these two allocations will differ because individuals will not fully internalize the effect that their actions have on both the spread of the virus and the stress on the healthcare system. In this respect our findings reinforce those of the recent contributions in the economics literature of Fenichel (2013), Farboodi, Jarosch, and Shimer (2020) and Toxvaerd (2020), who also adopt tools familiar to economists and show that incorporating behavioral responses reduces the spread of the virus. While the model presented in this Commentary is quite simple, it provides new insights into the potentially beneficial role of government policy that we wish to highlight. In the simulations that follow, the reduction in economic activity in response to the virus is similar across both the equilibrium and optimal allocations. The primary difference between the two is that in the equilibrium allocation activity returns to normal far too quickly, illustrating that lockdowns and other nonpharmaceutical interventions may be particularly important toward the middle and end of a pandemic.
General Description of Our Approach
To illustrate our methodology with an example more common in economic analysis, suppose that we wish to estimate the changes in government revenue and gross domestic product due to a proposed change in taxes on savings and labor income. The correct answer will obviously depend upon on how individuals alter their savings and labor supply in response to the policy. An analysis of such a proposal will often assume households’ decisions are the result of optimally choosing their current and future consumption and labor supply, given the constraints imposed by their budgets. To ensure that these choices are feasible for the economy as a whole, we assume that prices adjust so that supply equals demand in each market and that individuals expect such price adjustments when formulating their plans.
Although in this example households are responding to forecasted price changes, the methodology may be applied to a model of virus transmission. The key point is that we formed our prediction by assuming that individuals are forward-looking, that they make choices based upon their expectations of changes in their environment, and that these expectations are consistent with the behavior of everyone else. In the model of the proposed tax, households recognize that prices are collectively determined by aggregate demand and supply but unaffected by their individual behavior. In a similar vein, in our discussion we will assume individuals understand that the prevalence of the virus depends upon their aggregate behavior, but they view themselves as individually unable to alter its course.
In the model used in this Commentary, individuals have preferences over current and future values of a single variable representing their overall level of activity, but they fear the possibility of death. We assume that people prefer more activity to less, but that higher activity increases the probability of contracting the virus. In this way, individuals face a tradeoff and must weigh their desire for high activity against the associated risks to their future health. Furthermore, we explicitly build upon the SIR model in our assumptions regarding virus transmission. Specifically, the implied paths of infected and susceptible agents will coincide exactly with the SIR model in the special and extreme case in which individual behavior is not responsive to the prevalence of the virus. It is in this way that we believe the work of economists can complement the insights of the epidemiological literature, as the model presented here strictly generalizes the SIR framework.
Description of the Model
Our model builds upon the SIR model of Kermack and McKendrick (1927), in which a population of individuals is at any moment divided into three categories, Susceptible (S), Infected (I), or Removed (R).4 In this original model, infected individuals face constant probabilities of death or recovery, and the probability that a susceptible individual becomes infected on any day is assumed to be a (fixed) multiple of the number of infected individuals. Once recovered, an individual is assumed to be immune, unable to contract the virus again or transmit it to others. The transmission mechanism may be interpreted as one in which a large number of individuals randomly bump into one another every day, and that each meeting between an infected individual and a susceptible individual involves a fixed probability of the virus being transmitted. In this sense this baseline case fails to capture the fact that individuals may act to reduce such meetings if they fear contracting the virus.
We consider a fictional economy populated by a large number of identical individuals who at any moment make a single choice for their overall level of activity, represented by a number a lying in the unit interval [0, 1]. One may think of a as representing the amount of activity (either commercial or social) of the individual relative to their prepandemic level. We assume that individuals prefer high activity to low activity (they do not like being cooped up inside) but that high activity increases the probability of contracting the virus. The dynamics of disease propagation we adopt build upon a (slight generalization) of the aforementioned SIR framework, with individuals either susceptible (S), infected (I), recovered (R), or dead (D). The key difference is that we now assume that susceptible individuals become infected at a rate proportional to the number of meetings they have with infected individuals, and that this number of meetings is increasing in their choice of activity level. Formally, when susceptible and infected individuals take actions a1 and a2, respectively, population shares evolve according to the following set of equations:
(1) S1 = −βSIa1a2
I1 = βSIa1a2 − γI
R1 = γ(1 − δ(I ))I
D1 = γδ (I )I,
- Everyone chooses the highest level of activity regardless of the course of the disease (the baseline SIR model).
- Each individual acts in their own self-interest, taking as given the activity levels of everyone else (the equilibrium outcome).
- The government acts in the collective interest of society and dictates the activity levels of the susceptible individuals (the optimal outcome).
The first scenario is the SIR outcome and is completely described by setting a1 = a2 = 1 in the equations of (1). To describe the second, equilibrium scenario, we must specify the objectives and expectations of individuals. For objectives, we choose preferences satisfying three assumptions: individuals prefer high activity levels to low, prefer smooth changes in activity to abrupt and irregular changes, and care more about activity levels today than at points in the future. For expectations, we assume each individual believes themselves to be unable to affect the population shares of susceptible, infected, or recovered individuals and takes these shares as given when formulating a plan of activity. Formally, an equilibrium is a collection of plans for every individual such that the path of the virus expected by individuals coincides with that implied by their plans, and the plan of each agent maximizes their objectives. For the third, optimal scenario, we assume that the objective of the government is the sum of the objectives of the individual agents. The optimal scenario is the outcome if the government maximizes its objective by dictating activity levels through lockdowns and other nonpharmaceutical interventions.5 This differs from the second scenario because the government recognizes how the activity of one individual affects everyone else and adjusts individuals’ prescribed level of activity accordingly.
The first scenario served as a simple benchmark in much of the public commentary that appeared during the early stages of the pandemic. However, we believe the second scenario is more useful as it takes seriously the fact that individuals will likely take actions to reduce their exposure to a potentially fatal disease. In our opinion, the desirability of government action emerges from the difference between the second and third scenarios, since it makes clear how the recommendations of a government may differ from the actions of its constituents even when objectives coincide. Further, it is important to note that the outcome in the second scenario coincides with the baseline SIR model in the case in which individuals do not wish to alter their actions to avoid contracting the virus. A mathematical description of the model is given in the online appendix.
We now depict graphically how populations and activity levels differ across the above three scenarios for an example set of parameters. The parameters of the model are taken from estimates in the epidemiological literature and are subject to some uncertainty. Due to the degree of uncertainty surrounding these parameters and the model specification, we focus here upon those qualitative features of the model that appear robust to parameter choice.
We follow Farboodi, Jarosch, and Shimer (2020) and assume recovery takes 7 days on average and that the initial reproduction number (the average number of people infected by an individual at the start of the pandemic) is R0 = 3.1. Figure 1 plots optimal and equilibrium activity levels over time. The y-axis here is one possible measure of welfare, as it captures the extent to which the virus has led to a curtailment of activity. To understand this graph, one may think of it as describing the experience of two countries during the pandemic, one of which followed the second scenario, and the other of which followed the third.6 Even in this simple model, a number of interesting (and nonobvious) features emerge. First, in both the optimal and equilibrium allocations individuals do not change their activity levels in the beginning, but both exhibit an abrupt fall in activity shortly thereafter. Second, activity drops more sharply and for a longer period in the optimal allocation than in the equilibrium allocation, reflecting the fact that the government internalizes the effect individuals have on each other. Third, the difference between the two allocations is small near the early to middle part of the pandemic and large near the end, with activity returning to the initial (normal) levels much more rapidly in the equilibrium allocation than in the optimal allocation.
Figure 1. Optimal and Equilibrium Activity Levels
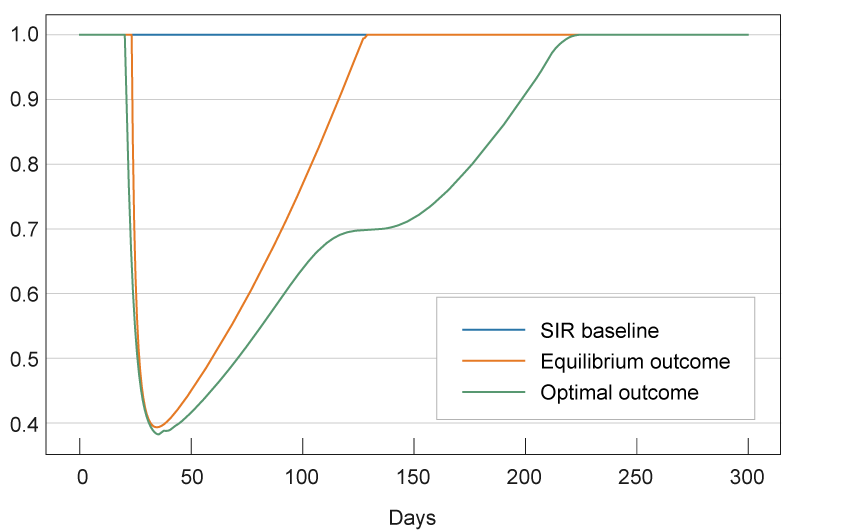
Source: Authors’ calculations. See online appendix for details.
This last point also illustrates that the length of the pandemic is not necessarily inversely related to the efficacy of the government intervention. Of the above three scenarios, the number of infected individuals falls to zero most quickly in the baseline SIR model in which activity levels are fixed throughout. However, this is also clearly the worst scenario of the above three, with the rapid fall in infected levels due only to the rapid movement of the virus through the population, leading to a high loss of life. For this reason, simply looking at the activity levels in figure 1 is insufficient to assess the merits of government intervention, since it does not capture the health risks incurred by the individuals in the economy. Figures 2 and 3 add to the above discussion by depicting the fractions of infected and dead individuals across the three scenarios. Figure 3 shows that incorporating individuals’ responses to the risk posed by the virus more than halves the number of deaths in this scenario relative to the baseline SIR. However, it still does not bring the number down to the optimal level, which again illustrates the benefits of government intervention.
Figure 2. Infection Rates over Time
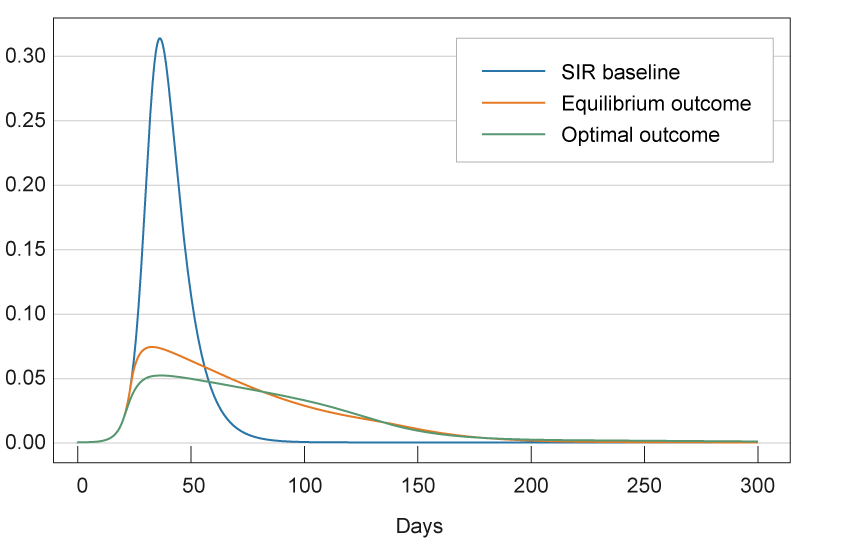
Source: Authors’ calculations. See online appendix for details.
Figure 3. Cumulative Deaths over Time
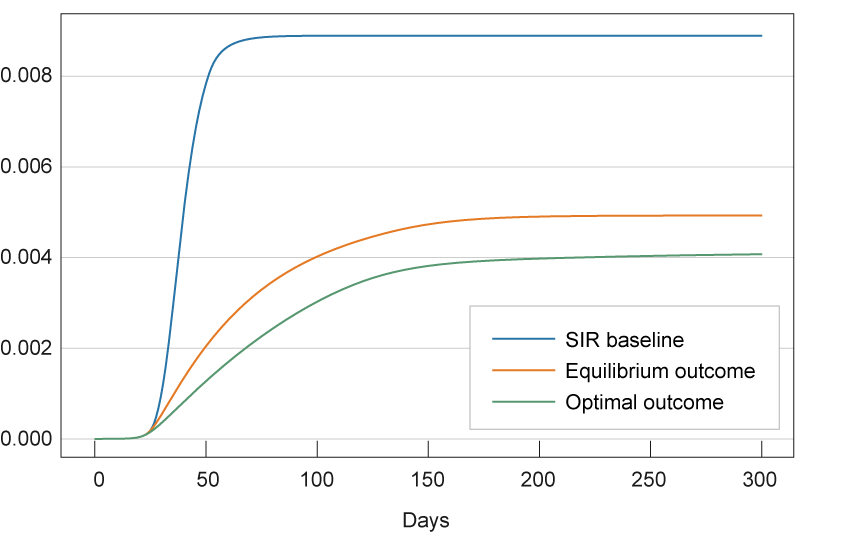
Source: Authors’ calculations. See online appendix for details.
Discussion
Our above discussion has deliberately adopted the transmission mechanism of the canonical SIR model in order to isolate the importance of modeling a behavioral response. It is therefore unable to capture the role that the network structure connecting individuals or various forms of heterogeneity within the population may play in shaping the course of the virus. Enriching the model along these dimensions could well increase the accuracy of the associated forecasts, but it would also lead to substantial complications, since the individuals would now need to form beliefs over the prevalence of the virus throughout multiple demographics and across different parts of the networks.
However, this issue provokes a natural question. Why do we need to go to the effort of positing a structural model of virus transmission with forward-looking agents and an notion of consistency as in the above equilibrium? Could we not simply proceed by comparing how infection rates vary across jurisdictions with the intensity of lockdowns (as in, for instance, Hsiang et al., 2020) and trading off the reduction in economic activity with some estimate of the lives saved? There are two reasons why such a model would not necessarily be an improvement over the approach we take, even if it is richer in many dimensions and more accurate in its forecast. First, fear of contracting the virus may lead people to change their behavior and mitigate the spread of the virus independent of government mandates. A comparison of the above kind may conflate the effect of intervention with the precautionary actions of individuals.
Second, and more importantly, even if this alternative approach provides accurate estimates for the immediate effects of intervention it leaves a number of key questions unanswered. For example, we might want to know how the effectiveness of government interventions varies with the prevalence of the virus, and estimates of the immediate effects of policy on disease propagation are only one part of this analysis. It is conceivable that an intervention may greatly reduce, but not eliminate the virus, resulting only in slower propagation but no reduction in total fatalities. Further, prescriptions for policy require one to balance the benefits of intervention with estimates of their costs, such as reduced economic activity or social isolation. In the absence of such costs, society would presumably be in a state of near-permanent lockdown to combat even the mildest outbreak. For these reasons we need both a model for how individual and government actions affect the propagation of the virus and an explicit notion of social welfare. Although simple, the notion of costs adopted in this Commentary is internally consistent, in the sense that in the optimal allocation the government acts in the interest of citizens at all times. Put another way, if presented with the option prior to the pandemic, all individuals would prefer to follow the recommendations in the above optimal allocation, if they could be assured that all susceptible individuals would do the same.
Conclusion
In this Commentary we have argued that the inclusion of behavioral responses by individuals adds an important dimension to the discussion of the ongoing COVID-19 pandemic. We build upon a standard epidemiological model in which the virus spreads randomly from meetings between susceptible and infected individuals, but we allow people to choose the frequency of these meetings based on their own assessment of the risk involved. We show that such a framework diminishes, but does not eliminate the role for government intervention. While it is reasonable to suppose individuals wish to protect themselves from the potentially fatal consequences of the virus, they will likely not fully internalize the effect their actions have on others in society.
We also believe it is worth emphasizing that every counterfactual argument about policy directed at the COVID-19 virus relies upon assumptions of behavioral responses, whether they are explicitly stated or left in the background. Implicit in statements such as “we could have saved more lives if ...,” or “the lockdowns didn’t save many lives because people were avoiding interactions anyway” is a theory of how private behavior alters the propagation of the virus.
The benefit of the approach in this Commentary is that the objectives of the fictional government planner in the optimal allocation are made explicit and coincide exactly with the aggregation of individual preferences. This clarifies the manner in which the tradeoffs facing an individual differ from those of society as a whole and allows us to explore how this divergence varies throughout the pandemic. In our numerical results we find that both the equilibrium and optimal allocations involve a sharp reduction in economic activity soon after the onset of the pandemic. The primary difference across the allocations is that from the point of view of a benevolent government acting in the interests of its constituents, in the equilibrium case activity returns to “normal” too quickly, suggesting that governments have a particularly important role to play in restricting activity beyond an initial short lockdown period.
The views authors express in Economic Commentary are theirs and not necessarily those of the Federal Reserve Bank of Cleveland or the Board of Governors of the Federal Reserve System. The series editor is Tasia Hane. This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. This paper and its data are subject to revision; please visit clevelandfed.org for updates.
Footnotes
- For surveys, see Hur and Jenuwine (2020) and Ellison (2020). Return to 1
- Craig et al. (2020). Return to 2
- See Keeling and Rohani (2008) for a textbook treatment account. Return to 3
- “Removed” refers to individuals who are removed from the susceptible and infected populations. The category includes individuals who have recovered, have died, or are immune to the disease. For textbook accounts of both the SIR model and other models common in epidemiology, we refer the reader to Hethcote (2000) and Keeling and Rohani (2008). Return to 4
- This exercise is therefore similar to the control problems of Alvarez, Argente, and Lippi (2020) and Farboodi, Jarosch, and Shimer (2020), except for the fact that the government does not treat infected and susceptible individuals identically. Return to 5
- Since the prevalence of the virus differs along the two paths, one cannot literally interpret the difference as a measure of inefficiency of activity levels at a point in time. Nonetheless, the fact that they differ captures the need for government intervention. Return to 6
References
- Alvarez, Fernando E., David Argente, and Francesco Lippi. 2020. “A Simple Planning Problem for COVID-19 Lockdown.” National Bureau of Economic Research, Working Paper No. 26981. https://www.doi.org/10.3386/w26981.
- Craig, Ben R., Tom Phelan, Jan-Peter Siedlarek, and Jared Steinberg. 2020. “Improving Epidemic Modeling with Networks.” Federal Reserve Bank of Cleveland, Economic Commentary, 2020-23. https://www.doi.org/10.26509/frbc-ec-202023.
- Ellison, Glenn. 2020. “Implications of Heterogeneous SIR Models for Analyses of COVID-19.” National Bureau of Economic Research, Working Paper No. 27373. https://www.doi.org/10.3386/w27373.
- Farboodi, Maryam, Gregor Jarosch, and Robert Shimer 2020. “Internal and External Effects of Social Distancing in a Pandemic.” National Bureau of Economic Research. Working Paper No. 27059. https://www.doi.org/10.3386/w27059.
- Fenichel, Eli P. 2013. “Economic Considerations for Social Distancing and Behavioral Based Policies during an Epidemic.” Journal of Health Economics, 32(2): 440–451. https://www.doi.org/10.1016/j.jhealeco.2013.01.002.
- Funk, Sebastian, Marcel Salathé, and Vincent A. A. Jansen. 2010. “Modelling the Influence of Human Behaviour on the Spread of Infectious Diseases: A Review.” Journal of the Royal Society Interface, 7(50): 1247–1256. https://www.doi.org/10.1098/rsif.2010.0142.
- Hethcote, Herbert W. 2000. “The Mathematics of Infectious Diseases.” SIAM Review, 42(4), pp. 599–653. https://www.doi.org/10.1137/S0036144500371907.
- Hsiang, Solomon, Daniel Allen, Sébastien Annan-Phan, Kendon Bell, Ian Bolliger, Trinetta Chong, Hannah Druckenmiller, Luna Yue Huang, Andrew Hultgren, Emma Krasovich, Peiley Lau, Jaecheol Lee, Ester Rolf, Jeanette Tseng, and Tiffany Wu. 2020. “The Effect of Large-Scale Anti Contagion Policies on the COVID-19 Pandemic.” Nature, 584: 262–267. https://www.nature.com/articles/s41586-020-2404-8.
- Hur, Sewon, and Michael Jenuwine. 2020. “Lessons on the Economics of Pandemics from Recent Research.” Federal Reserve Bank of Cleveland, Economic Commentary, 2020-11. https://www.doi.org/10.26509/frbc-ec-202011.
- Keeling, Matt J., and Pejman Rohani. 2008. Modeling Infectious Diseases in Humans and Animals. Princeton University Press. https://www.doi.org/10.2307/j.ctvcm4gk0.
- Kermack, William Ogilvy, and A. G. McKendrick. 1927. “A Contribution to the Mathematical Theory of Epidemics.” Proceedings of the Royal Society of London, Series A, Mathematical, Physical, and Engineering Sciences, 115(772): 700–721. https://www.doi.org/10.1098/rspa.1927.0118.
- Toxvaerd, Flavio M. O. 2020. “Equilibrium Social Distancing.” University of Cambridge, Cambridge Working Papers in Economics No. cwpe2021. https://www.doi.org/10.17863/CAM.52489.
Suggested Citation
Craig, Ben R., Tom Phelan, Jan-Peter Siedlarek, and Jared Steinberg. 2021. “Modeling Behavioral Responses to COVID-19.” Federal Reserve Bank of Cleveland, Economic Commentary 2021-05. https://doi.org/10.26509/frbc-ec-202105
This work by Federal Reserve Bank of Cleveland is licensed under Creative Commons Attribution-NonCommercial 4.0 International
- Share




